Sutinaa ja pöhinää jaksollisessa järjestelmässä III
Lohkon d ylimmälle riville, keskiviivan oikealle puolelle sijoittuu viisi tärkeää alkuainetta: rauta, koboltti, nikkeli, kupari ja sinkki. Kolmen ensimmäisen kemialliset merkit ovat Fe–Co–Ni, eli melkein ”Pe–co–ni” (makkara), jonka jälkeen tuleekin KU(pari)SI(nkki), eli Cu–Zn. Miksi sitten pekoni-makkara, eikä pelkkä pekoni? Yksi syy löytyy elektronegatiivisuusarvoista: alkuaineilla Fe–Co–Ni on kaikilla sama elektronegatiivisuusarvo (1.8)–(1.8)–(1.8), vaikka arvon pitäisi periaatteessa kasvaa oikealle mentäessä. Aineilla on myös kaikilla samat hapettumisluvut +II ja +III, eli ne muodostavat kummallisen tiiviin ”pötkön”, josta ainakin itselleni tulee turhankin sitkeästi mieleen nuo bensa-asemilla ja R-kioskeilla lasivitriinin takana hitaasti ja surullisesti pyörivät pekoniin rullatut makkarat.
Tätä Fe–Co–Ni:n ”pötkömäisyyttä” lisää vielä se kummallinen tosiasia, että jaksollisessa järjestelmässä tämä makkara lepää aivan tasaisen, suorakulmaisen ”jalometallisen” (Pd, Pt, Ir) tarjottimen päällä. Kuten sanottu, elektronegatiivisuusarvohan periaatteessa kasvaa oikealle ja ylöspäin mentäessä. Kuitenkin tämän kolme yksikköä pitkän pekoni-makkaran alla on täysin tasainen 2×3 alusta, jonka alueella elektronegatiivisuusarvo ei näytä muuttuvan miksikään, vaan on kauttaaltaan suorastaan epäilyttävän tasaisesti 2.2.
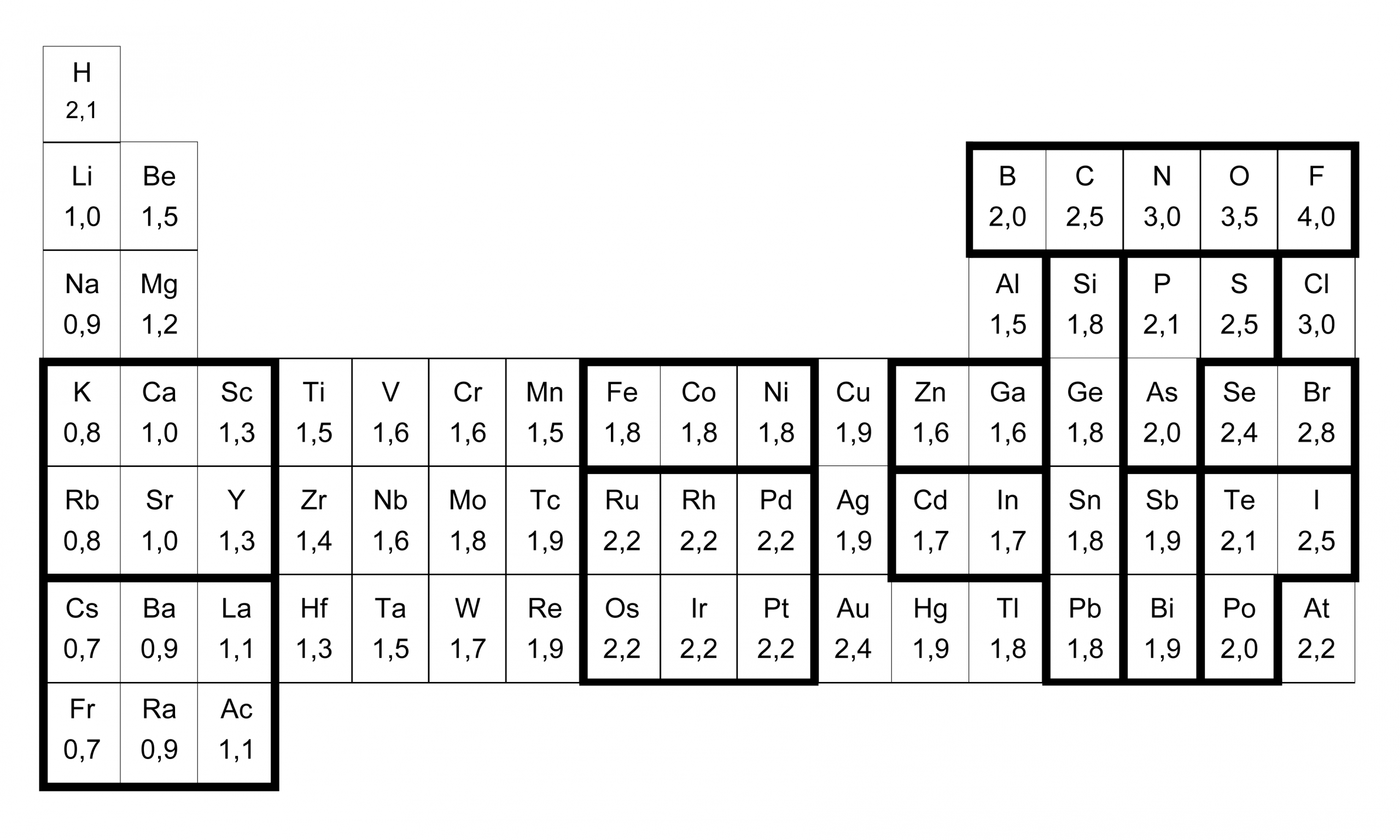
Toisaalta vielä pahemmin elektronegatiivisuusarvon systemaattista muutosta näyttävät uhmaavan 3. pääryhmän alkuaineet, joiden elektronegatiivisuusarvot eivät suinkaan kasva alhaalta ylöspäin mentäessä, vaan päinvastoin pienenevät tasaisesti aina booriin asti: (1.8)–(1.7)–(1.6)–(1.5)–(2.0). Viereisen 4. pääryhmän kohdalla tilanne jo stabiloituu, kun koko pylvään arvot aina hiileen asti ovat samat: (1.8)–(1.8)–(1.8)–(1.8)–(2.5). Elektronegatiivisuusarvojenhan puolesta tämä ”harmaa” lyijy–tina–germanium–pii–pylväs on kuin vertikaalinen toisinto tuosta horisontaalista Fe–Co–Ni–makkarasta.
Vegaanien lukijoideni helpotukseksi siirrän nämä nakit ja makkarat ainakin hetkeksi syrjään ja tyydyn lyhyesti toteamaan, että d-lohkon ylimmälle riville, raudan vasemmalle puolelle on näköjään pysäköity rivi kiiltäviä autoja: Sc–Ti–V–Ch–Mn, eli Scan-Titan, Volvo, ja Chrysler-Mini.
Nouseva Hopeanuoli
Hapetusluvut poikkeavat alkuaineiden monista muista ominaisuuksista aivan olennaisesti siinä, että ne kuuluvat ennemmin ”toimistoon” kuin ”laboratorioon”. Hapetusluvut ovat tietyssä mielessä täysin fiktiivisiä ja ”kirjanpidollisia” arvoja, niitä kun ei voida kokeissa mitata. Lisäksi saman molekyylin samalle atomille voidaan jopa eri hapetusluku-sääntöjä käyttämällä saada erilaiset (!) hapetusluvut, ja molemmat ovat kuitenkin yhtä ”oikein”.
Hapetuslukujen hyödyllisyyttä tai loogisuutta vastaan ei voi oikein mitään kovin painavia argumentteja esittää. Toisaalta, kun esimerkiksi MAOL:n taulukoista tarkastelee alkuaineiden yleisimpiä hapetuslukuja, niin mieleen palautuu pakostakin tarina astronomista, joka esitteli kuninkaalleen suurta maailmanjärjestelmää. Astronomi kertoi huolellisesti ja tarkkaan, kuinka monimutkaisia ympyräliikkeitä, episyklejä, hyposyklejä, deferenttejä yms. yhdistelemällä planeettojen liikkeet saadaan vastaamaan havaintoja. Kuningas kuunteli esitystä hiljaa ja kiinnostuneena. Kun astronomi oli päässyt esityksensä loppuun kuningas mietti hetken ja sanoi: ”Voi olla, että luoja on kaiken juuri noin asettanut, mutta jos minulta kysytään, niin paljon yksinkertaisempi olisi kyllä riittänyt!”
Samansuuntaisia ajatuksia kehittyy helposti ihmisessä, joka yrittää saada tolkkua alkuaineiden hapetusluvuista, edes niistä kaikkein tavallisimmista. Ryhmät 1, 2 ja 3 ovat tietysti aivan helppoja, samoin 3. pääryhmä eli B, Al, Ga, jne., mutta sitten yksinkertaiset säännöt ja kuviot tuntuvat karkaavan aika nopeasti näkyvistä. Yksittäisiä järjestyksen saarekkeita pilkottaa kyllä sieltä täältä, esim. ”rautaiset” hapetusluvut +II ja +III tuon Fe–Co–Ni–makkaran sisällä. Makkaran vierestä löytyy myös selkeä 2×3 alue, joka koostuu kahdesta yhteen liitetystä L-muotoisesta palikasta. Ylemmän palikan sisällä kaikkien alkuaineiden (Cu, Zn, Cd) hapetusluku on +II ja mausteena tuo kuparille myös mahdollinen +I. Alemman palikan sisällä (Ag, Hg, Au) kaikilla alkuaineilla on hapetusluku +I, mutta sen lisäksi (järjestyksessä Ag–Hg–Au) luvut +I, +II, +III.
Jo tässä yksinkertaisessa 2×3 alueessa tulee hyvin esille hapetuslukujen systemaattisten sääntöjen ja poikkeuksien epämukava rajankäynti. Esimerkiksi tuossa jälkimmäisessä palikassa hopealle tulee annettua ikään kuin ”kahteen kertaan” arvo +I, mikä ei liene niin suuri ongelma, mutta kuitenkin. Eräs lisätuki tälle alueelle on lyhyt kolmen ruudun läpi diagonaalisesti nouseva ”Hopeanuoli” Ag–Zn–Al, joka sisältää vain hapetusluvut +I, +II, +III. Vaikka tämä oikealle nouseva Hopeanuoli ei liene lähimainkaan Salvarsanin veroinen ”silver bullet”, niin onhan tämäkin tyhjää parempi diagonaalituki hapetusluvuille.
Kolmikon Ag–Zn–Al erityisen hyviä puolia ovat, että nämä metallit ovat aika usein esillä kemian hapetuslukuja tarvittavissa laskuissa ja että niillä kaikilla on vain yksi hapetusluku. Täsmennän hieman epäkohteliaasti tähän väliin, että kun puhun ”kemiasta” ja ”vain yhdestä hapetusluvusta”, niin tarkoitan lukio-tason kemiaa. Tiedän, että korkeammassa ja teoreettisemmassa kemiassa alkuaineista voidaan erikoisolosuhteissa saada aikaan jos jonkinlaisia yhdisteitä, joissa myös hapetusluvut voivat olla hyvinkin eksoottisia, etten sanoisi jopa patologisia tässä puheena oleviin lukuihin verrattuna.
Jyvät ja Akanat
Löytyykö siis mitään selkeää ja helppoa hapetuslukuihin liittyvää sääntöä, joka auttaisi muistamaan tai edes vähän paremmin ymmärtämään alkuaineita? Melkein nolottaa kertoa tätä, mutta vaikka olin kuinka yrittänyt tutkia ja opetella edes joitakin hapetuslukuihin mahdollisesti liittyviä säännönmukaisuuksia, niin eräs hyvinkin ilmeinen säännönmukaisuus jäi minulta pitkäksi aikaa täysin huomaamatta. Lisäksi alkuaineiden joukossa on esimerkiksi typen (N) kaltaisia kameleontteja, jotka näyttävät voivan saada melkein minkä tahansa hapetusluvun. Tällainen ailahteleva ja häiritsevä käytös näyttää olevan erityisen yleistä juuri siirtymämetallien keskuudessa. Lopulta kuitenkin huomasin pääryhmiin soveltuvan yksinkertaisen säännön:
Joka toisen pääryhmän alkuaineilla on vain parillisia ja joka toisen pääryhmän alkuaineilla on vain parittomia hapetuslukuja! Heureka!
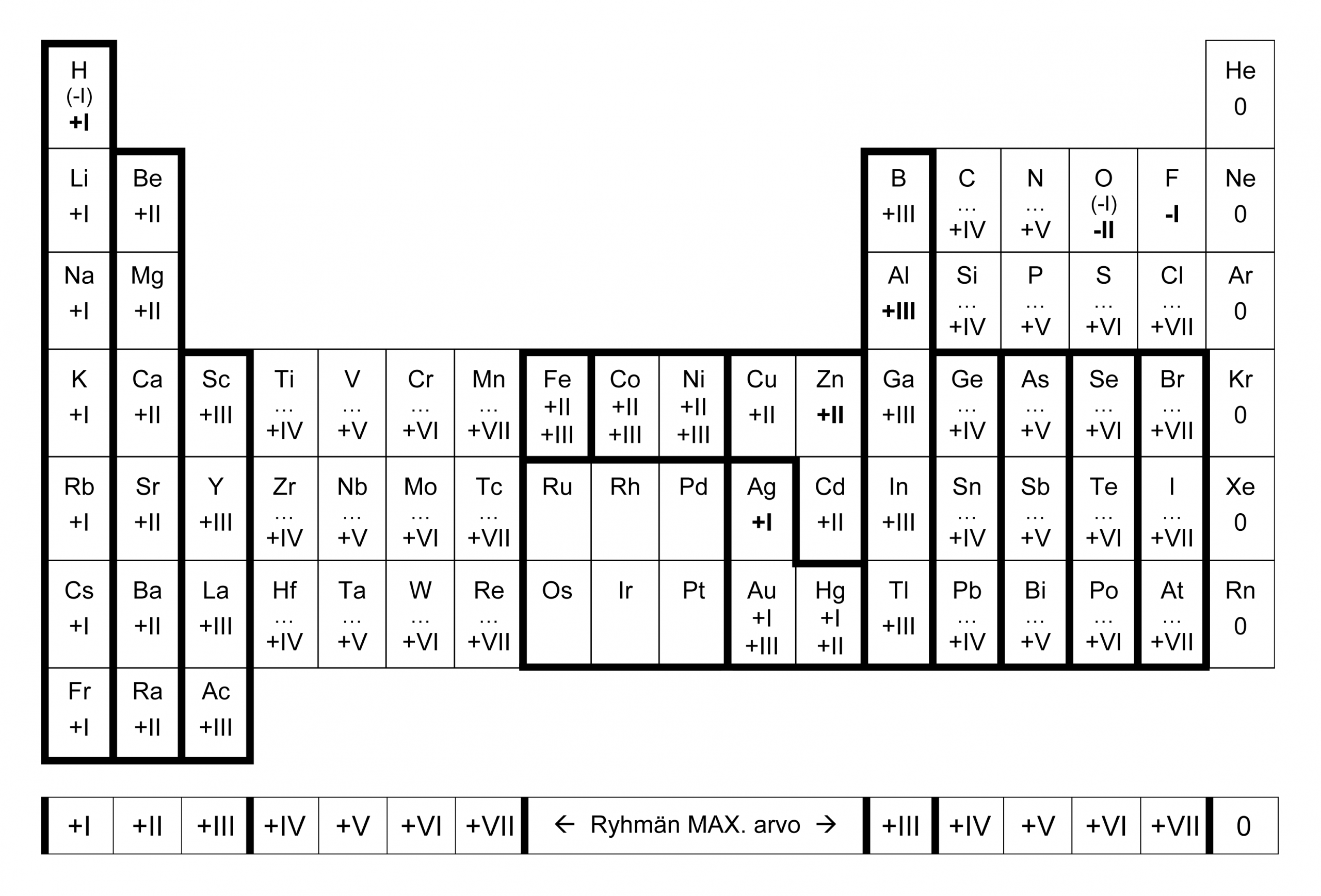
Tuntuu uskomattomalta, miten näinkin yksinkertaisen tiedon esiin kaivaminen ihan selvästä taulukosta oli kovan työn ja tuskan takana. En tiedä oliko vaikeuden syynä se, että roomalaisin numeroin (kirjaimin) ilmaistut hapetusluvut näyttävät usein kulmikkailta harakan varpailta tai pieniltä ja teräviltä piikkilangan pätkiltä, eivät siis lyhyesti sanottuna kovin houkuttelevilta tutkimuskohteilta. En muista, että tätä joka–toinen–sääntöä olisi erikseen lukion kemian kirjoissa kerrottu tai ainakaan painotettu, mutta jos oli, niin en asiaa ainakaan itse huomannut.
Tietenkin jokaiseen joukkoon mahtuu aina muutama ilonpilaaja ja tässä tapauksessa tuo ikävä rooli lankeaa vedylle (H), hapelle (O) ja jo kertaalleen haukutulle typelle (N). Vahinko ei tosin ole kovin suuri, sillä poikkeukset rajoittuvat vain muutamaan tapaukseen: vedyn hapetusluku yhdisteissä on tavallisesti +I mutta metallien kanssa –I ja hapen hapetusluku yhdisteissä on tavallisesti –II paitsi peroksideissa –I, joissa happiatomi on liittyneenä toiseen happiatomiin yksinkertaisella kovalenttisella sidoksella. Erikoistapauksessa jopa hapen hapetusluku voi muuttua positiiviseksi, jos se joutuu tekemisiin kaikkein elektronegatiivisimman aineen, fluorin (F) kanssa.
Näitä kolmea pientä poikkeusta lukuun ottamatta kaikki muut pääryhmien alkuaineet näyttävät siis noudattavan tuota joka–toinen–ryhmä–parillinen–joka–toinen–ryhmä–pariton–sääntöä. Vaikka en asiaa syvällisemmin ymmärrä, niin sääntö tuntuu loogiselta, kun ajattelen, että yhdelle orbitaalille mahtuu korkeintaan tasan kaksi erimerkkiset spinit omaavaa elektronia. Käsittääkseni yksi esimerkki tällaisesta elektronien pariutumisesta ovat ”vapaat” elektroniparit, jollainen esimerkiksi ammoniakki-molekyylin tapauksessa taivuttaa molekyylin muotoa tasomaisesta kolmiosta hieman avaruudellisempaan, pyramidin muotoon, tai vesimolekyylin happiatomilla olevat kaksi vapaata elektroniparia, joita ilman vesimolekyyli olisi kai muodoltaan hiilidioksidin tapaan lineaarinen.
Näitä elektronipareja vasten katsottuna tuntuu jokseenkin ymmärrettävältä, että jos atomi X:llä on jossain yhdisteessä pariton määrä sidoksia, niin myös muissa yhdisteissä sillä on pariton määrä sidoksia, vaikka sidosten absoluuttinen lukumäärä muuttuisi. Ja sama parillisten sidosten tapauksissa. Myös tieto sivuryhmien atomien osittain täyttyneestä d-alakuoresta tuntuu sopivan siihen, että useilla sivuryhmien alkuaineilla on sekä parillisia että parittomia hapetuslukuja.
Näin alkuaineiden yleisimpien hapetuslukujen taulukko alkoi hahmottua itselleni hieman loogisempana kokonaisuutena; jokaisen pääryhmän numero kertoo siihen kuuluvien alkuaineiden suurimman mahdollisen positiivisen hapetusluvun ja vedyn, hapen ja typen muutamaa poikkeusta lukuun ottamatta kaikki muut pääryhmien alkuaineet näyttävät noudattavan tuota joka–toinen–sääntöä, eli jos alkuaineen X atomilla on pariton hapetusluku, niin sen loputkin hapetusluvut ovat parittomia. Ja sama parillisille. Tietenkään ei sovi unohtaa, että vain puoli- ja epämetalleilla voi olla sekä positiivisia että negatiivisia hapetuslukuja, kun taas metalleilla hapetusluku on (lukio-tason kemiassa) aina positiivinen.
Lue myös kirjoittajan aiemmat kirjoitukset
Sutinaa ja pöhinää jaksollisessa järjestelmässä I (19.11.2019)
Sutinaa ja pöhinää jaksollisessa järjestelmässä II (3.12.2019)
Aminoffit ja Möttöset (22.10.2019)
Aloituskuva: isak55 / Shutterstock.com