Singapore Mathin menestystarina

Singapore on tullut tunnetuksi siitä, että se on vuodesta 1995 lähtien ollut kaikissa TIMMS-testeissä ja PISA-testeissä neljän parhaan maan joukossa, useimmiten ykkösenä. Singapore on aasialainen kaupunkivaltio, jonka asukasluku on yli 5,5 miljoonaa, mutta pinta-ala vain 722 km². Lapset aloittavat koulunkäynnin 7-vuotiaina. Kaikille yhteinen alakoulun matematiikka käsittää luokat 1-4. Luokilla 5-6 oppilaat voivat valita perusmatematiikan (Standard Maths) tai helpomman kurssin (Foundation Maths). Toisella asteella lahjakkaimmat oppilaat voivat valita vaativan matematiikan kurssin, joka on tiivistetty neljään vuoteen. Helpommat kurssit kestävät viisi vuotta ja tarjolla on neljä eri vaihtoehtoa.

Vuonna 1980 Singaporessa ei ollut omia opetussuunnitelmia eikä oppimateriaalituotantoa, vaan oppimateriaalit tuotiin ulkomailta ja ne noudattivat kyseisen maan opetussuunnitelmaa. Vuonna 1981 Singaporen hallintoviranomaiset perustivat työryhmän, jonka tehtävänä oli laatia matematiikan opetussuunnitelma luokille 1-6 sekä sitä noudattavat oppikirjat. Työryhmä tutustui maailman johtavien oppimistutkijoiden teorioihin matematiikan oppimisesta. He tutustuivat myös eri maiden matematiikan opetussuunnitelmiin ja oppimateriaaleihin sekä niillä saavutettuihin oppimistuloksiin.

Työryhmä laati opetussuunnitelmat, joissa keskeinen tavoite on opettaa harvoja käsitteitä syvällisesti, jotta ne ymmärretään ja opitaan käyttämään niitä . Matematiikan käsitejärjestelmää rakennetaan osa-alue kerrallaan, eikä spiraalia käytetä. Opetettavat asiat kerrotaan opetus­suunnitelmissa tarkasti.  Singaporelainen malli on vastakohta sille, että opetetaan useita käsitteitä ja malleja kohtaamalla ja pohjustamalla ja tuodaan niihin seuraavana vuonna vähän lisää.

Menetelmän idea

Singaporen menetelmään kuuluu keskeisiin käsitteisiin tutustuminen aluksi konkreettisten välineiden avulla kokeillen, pohtien ja perustellen. Välineet voivat olla esimerkiksi kymmenjärjestelmävälineitä ja yksikköpohja. Myös käsitteiden väliset yhteydet ovat tärkeitä. Konkreettisen välineillä tutkivan vaiheen jälkeen opiskeltavaa asiaa mallinnetaan kuvamallilla, usein palkkimallilla (bar model), joka sopii hyvin monenlaisten tilanteiden mallintamiseen.

Kuvamallin avulla päätellään sopiva ratkaisutapa, lasketaan ratkaisu ja verrataan sitä tehtävään. Päätellään, onko saatu vastaus järkevä. Ongelmanratkaisu etenee konkreettisesta vaiheesta kuvamallin kautta symbolivaiheeseen.

Esimerkki palkkimallin käytöstä monivaiheisen tehtävän ratkaisemisessa. Tehtävä on ”Singapore Math’in” viidennen luokan oppikirjasta.

”Rouva Chen leipoi piirakoita. Hän myi niistä 3/5 aamupäivällä. Iltapäivällä hän myi lopuista ¼. Hän myi aamupäivällä 200 piirakkaa enemmän kuin iltapäivällä. Kuinka monta piirakkaa hän oli kaikkiaan leiponut?”

Palkki kuvaa kaikkia piirakoita, joista hän myi aamupäivällä 3/5.

Iltapäivällä hän myi lopuista ¼. Jaetaan loppuosa neljään yhtä suureen osaan.

Jaetaan aamupäivän osuus yhtä suuriin osiin kuin iltapäivä, jolloin osia on kaikkiaan 10. Aamupäivällä myytyjä piirakoita oli 200 enemmän kuin iltapäivällä.  Kuvasta näkee, että yksi sininen ruutu vastaa yhtä punaista ruutua. Punaisia ruutuja on 5 enemmän kuin sinisiä. Jos 200 piirakkaa jaetaan viiteen osaan, saadaan 40 piirakkaa.

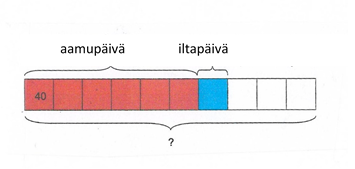
Koska 1/10 on 40 piirakkaa, kokonaismäärä eli koko palkki on 10 x 40 = 400. Kuvasta näkee myös, että hän myi kaikkiaan 7 x 40 = 280 piirakkaa. Myymättä jäi 3 x 40 = 120 piirakkaa.

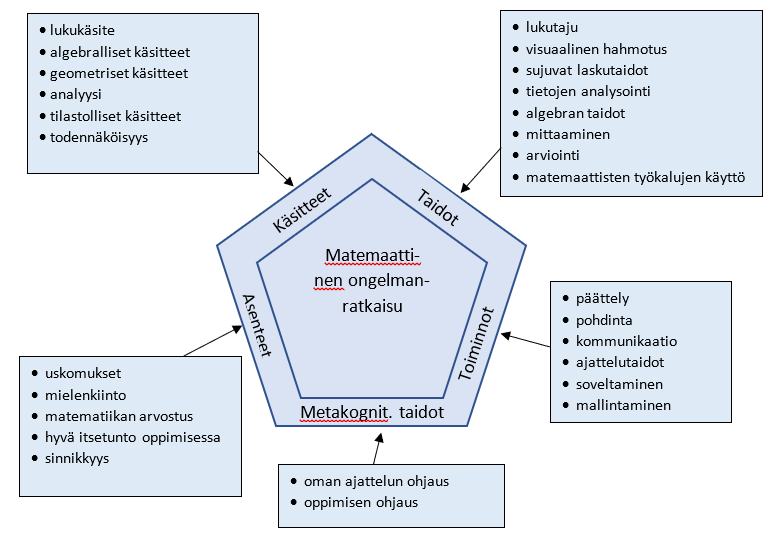
Matematiikan oppimisen osa-alueita ja tavoitteita työryhmä kuvasi viisikulmiomallilla. Matematiikan opetuksen tärkein tavoite on matemaattisen ajattelun ja ongelmanratkaisun oppiminen. Siksi ongelmanratkaisu on tavoitteita kuvaavan viisikulmion keskipisteessä. Sitä ympäröi viisi osa-aluetta eli käsitteet, taidot, toiminnot, metakognitiiviset taidot ja asenteet.

Singaporelainen tohtori Berinderjeet Kaur sanoo, että he ottivat parhaat puolet sekä idän että lännen menetelmistä. Selvitystensä pohjalta työryhmä laati materiaalin Primary Mathematics. Singaporen opetusministeriö halusi kouluihin myös muita vaihtoehtoisia oppimateriaaleja ja se vapautti 1990-luvun alussa peruskoulun oppikirjamarkkinat yksityiselle kilpailulle.

Oppimateriaalijärjestelmä

Kilpailun vapauduttua paikallinen yksityinen kustantaja, Marshall Cavendish, ryhtyi kustantamaan laajaa matematiikan oppimateriaalia. Hän tuotti lyhyessä ajassa kovakantiset oppikirjat, työkirjat ja opettajan kirjat luokille 1-6. Lisäksi sarjaan kuului molempiin suuntiin eriyttävää materiaalia. Kirjat noudattivat Singaporen uusien opetussuunnitelmien sisältöjä sekä viisikulmion tavoitteita.

Cavendishin julkaisemassa oppimateriaalissa jokaiselle luokka-asteelle on kaksi neliväristä teoriakirjaa ja kaksi yksiväristä työkirjaa, jotka ovat kertakäyttöisiä. Kirjojen kuvat ovat isoja ja niitä on paljon, joten kirjat ovat paksuja. Ne ovat myös hyvin selkeitä. Samat elementit; palautetaan mieleen, opitaan, harjoitellaan, tutkitaan, pohditaan ja testataan, toistuvat eri kirjoissa ja eri luokka-asteilla.

Opettajalle on tarjolla jokaiselle luokka-asteelle kaksi opettajan kirjaa, joissa ohjataan käsitteiden opettamiseen toiminnallisesti välineitä käyttäen. Oppaissa neuvotaan myös, miten on järkevää toimia viisikulmion kaikkien osa-alueiden tavoitteiden saavuttamiseksi. Opettajan materiaalissa on myös eriyttävää materiaalia erilaisille oppilaille sekä materiaalia oppimisen arviointiin.

Oppimistulokset olivat hämmästyttäviä. Vuonna 1995 järjestettiin maailman ensimmäinen TIMMS-testi (Trends in International Mathematics and Science Study) ja Singaporen oppilaat olivat heti kärkipaikalla. Kaikissa neljän vuoden välein järjestettävissä testeissä 1995-2019 Singapore on ollut neljän parhaan joukossa, kärkipaikalla vuosina 1999, 2003 ja 2015. Myös kansainvälisissä PISA-testeissä (Programme for International Student Assessment) Singapore on aina kuulunut maailman neljän parhaan maan joukkoon. Viimeisimmissä PISA-testeissä 2018 Singapore oli maailman toiseksi paras.

Opettajan rooli

Singaporessa uskotaan, että oppimisen edellytys on, että opettaja opettaa matematiikkaa. Opettaja jäsentelee tiedot, antaa oppimistehtävät ja ohjaa kommunikaatiota. Opettaja myös arvioi jatkuvasti oppimista monipuolisesti ja antaa oppilaille palautetta. Opettaja on luokassa auktoriteetti, eikä tavoitteena ole vastuun siirto oppilaille tai oppilaiden laaja valinnanvapaus oppimistavoitteiden suhteen. Opetukseen kuuluu avoimia ongelmia ja luovuutta kehittäviä tehtäviä, mutta opettaja varmistaa, että kaikki toiminta luokassa tähtää matematiikan oppimiseen ja ajattelun kehittämiseen. Matematiikan opiskelun ei tarvitse olla hauskaa tai helppoa. Motivaatio syntyy oppimisesta.

Opetussuunnitelmissa annetaan opettajalle opetuksen kolme keskeistä periaatetta:

1. Opetuksen tavoitteena on oppiminen, oppimisen tavoitteena on ymmärrys, ymmärtämisen tavoitteena on päättelytaito, soveltaminen ja kaiken ytimessä ongelmanratkaisu.
2. Opetuksen tulee rakentaa oppilaiden tietojärjestelmää. Opetus lähtee oppilaiden kokemuksista ja kiinnostuksesta ja ohjaa heidät aktiiviseen ja pohtivaan oppimiseen.
3. Opetus yhdistää matematiikan oppimisen todelliseen maailmaan, käyttää tietotekniikkaa ja painottaa 2000-luvulla tarvittavia valmiuksia.

Opettaja ohjaa positiivisten asenteiden syntymiseen ja myönteisten oppimiskokemusten saamiseen matematiikan opiskelussa. Onnistumiskokemukset vahvistavat oppilaan itsetuntoa. Hyvin opitut käsitteet ja taidot antavat varman pohjan uusien käsitteiden ja taitojen oppimiselle.

Menetelmä vaatii opettajalta hyvää matematiikan osaamista ja myös hyvää opetusmenetelmien tuntemusta ja taitoa ohjata oppilaita. Siksi opettajat tarvitsevat aika ajoin täydennyskoulutusta. Menetelmä antaa myös opettajille onnistumisen kokemuksia sekä hyvien oppimistulosten että innostuneiden oppilaiden kautta.

Oppilaat

Tietokoneet ja mobiililaitteet ovat kiinteästi mukana menetelmässä. Oppilaat kokevat matematiikan opiskelun mielekkäänä ja palkitsevana. Singaporessa oppilaat näkevät yleensä menestymisen koulussa velvollisuudekseen, joka edellyttää kovaa työntekoa. Vanhemmilla on oikeus odottaa hyviä tuloksia, koska he maksavat kalliita lukukausimaksuja. Kaikissa kouluissa on lukukausimaksu, parhaissa muita korkeampi. Koulunkäyntiin kuuluu usein myös lisäopintoja koulutuntien jälkeen. Varsinkin matematiikassa ne ovat yleisiä.

Singaporelainen matematiikan oppimisen tutkija, tohtori Berinderjeet Kaur esittelee vuoden 2018 ICME-kongressin (International Congress of Mathematics Education) luennossaan singaporelaisia tutkimuksia eri opetusmenetelmistä. Hän toteaa, että aasialainen opetusmalli on sisältöorientoitunutta ja kokeiden ohjaamaa. Se on myös opettajajohtoista. Opettaja selittää asioita, havainnollistaa välineillä, esittää uusia asioita ja antaa ohjeita. Oppilaat harjoittelevat tunnilla itsenäisesti tai ryhmissä. Samalla opettaja antaa palautetta oppilaille, ryhmille ja koko luokalle.

Kaur kertoo myös tutkimuksesta, jossa haastateltiin 59:ää oppilasta siitä, millainen matematiikan tunti on heidän mielestään hyvä. Hyvän oppitunnin elementtejä olivat oppilaiden mielestä:

• Opettaja selittää selvästi uudet käsitteet ja toiminnan vaiheet.
• Opettaja avaa vaikeita asioita havainnollistamalla välineillä tai arkielämän esimerkeillä.
• Kerrataan aikaisemmin opittua.
• Opettaja antaa palautetta onnistumisesta oppilaalle, ryhmälle tai koko luokalle.
• Opettaja antaa selkeitä ohjeita tuntitehtävistä tai kotitehtävistä.
• Opettaja antaa mielenkiintoisia tehtäviä tai ongelmia yksilöille tai ryhmille.
• Opettaja antaa riittävästi kokeisiin valmentavia harjoituksia.

Oppilaiden käsitykset hyvästä oppitunnista kertovat aasialaisten oppilaiden kaipaavan havainnollista ja selkeää opetusta ja ohjausta. He myös arvostavat nopeaa palautetta työstään. He haluavat tietää, mitä heiltä odotetaan ja ovat valmiita tekemään töitä sen saavuttamiseksi.

Singapore Math uudistuu

Singaporessa tulivat voimaan uudet matematiikan opetussuunnitelmat vuonna 2012. Sisällöissä ei ollut suuria muutoksia. Myös tavoitteiden viisikulmiomalli on entisellään. Digitaalisten työkalujen merkitys opetuksessa on lisääntynyt. Huomiota on kiinnitetty matemaattisen mallintamisen lisäämiseen. Globaaleihin ongelmiin, kuten ilmastonmuutokseen ja ympäristöongelmiin, tarvitaan laajoja ratkaisumalleja. Tietokoneet mahdollistavat yhä vaativampien matemaattisten mallien kehittelyn ja käyttämisen. Siksi mallintamista täytyy opiskella jo koulussa. Tämä vaatii ongelmanratkaisua ja luovuutta.

Singapore Math leviää maailmalla

Singaporen hyvät oppimistulokset herättivät muiden maiden mielenkiinnon Singaporen opetusmenetelmiä kohtaan, ihan samoin kuin Suomen menestys herätti mielenkiintoa meidän opetusmenetelmiämme kohtaan. Singaporella oli näyttää selkeät opetussuunnitelmat, kompakti ja uskottava tavoitemalli viisikulmiona sekä oppimateriaalijärjestelmä, jossa opetussuunnitelmat ja tavoitteet oli otettu huomioon. Koska Cavendishin kustantamat Singapore Math kirjat olivat englanniksi, ne otettiin käyttöön ensin Yhdysvalloissa kotikouluissa.

Menetelmä on levinnyt Aasian ulkopuolella Yhdysvaltojen lisäksi ainakin Britanniaan, Australiaan, Kanadaan ja Israeliin. Oppimateriaaleista on tehty eri maiden opetussuunnitelmiin sovitetut versiot, jotka on laadittu yhdessä singaporelaisten asiantuntijoiden kanssa ja painettu Singaporessa. Yhdysvalloissa käytettävä sarja on nimeltään Math in Focus ja sen alkulehdillä kerrotaan oppilaille näin: ”Tämä oppikirja noudattaa menetelmää, joka on lähtöisin Singaporesta. Se perustuu asioiden perusteelliseen tutkimiseen ymmärryksen saavuttamiseksi. Palkkimallin avulla sanallisten ongelmien ratkaisu tulee olemaan helppoa. Tulet yhdistämään loogisen ajattelun, matemaattiset taidot ja käsitteiden ymmärtämisen kohdataksesi uusia haasteita ongelmanratkaisussa. Tulet puhumaan matematiikasta, toimimaan konkreettisilla välineillä ja perustelemaan ratkaisujasi.”

Eri maissa on raportoitu menetelmän ansiosta parantuneita oppimistuloksia. Singaporen tasolle ei muualla vielä ole päästy. Se on ymmärrettävää, koska pelkkä opetusmenetelmä ei takaa oppimistuloksia. Eivätkä opettajat pysty hetkessä sisäistämään menetelmää, joka poikkeaa paljon heidän aiemmin käyttämästään menetelmästä. Myöskään oppilaat eivät koe laajasti yhtä suurta arvostusta matematiikkaa kohtaan tai yhtä suurta motivaatiota menestyä matematiikan opinnoissa kuin singaporelaiset oppilaat.

Menestyksen ydin?

Singaporen menetelmän keskeinen ominaisuus on, että sisällöt ja tavoitteet on tarkasti määritelty ja ohjattu niin opettajalle kuin hänen kauttaan oppilaille. Koulut eivät tee omia opetussuunnitelmia, eivätkä valitse erilaisia oppisisältöjä. Myös oppimateriaalit ovat samat ja kaikki käyttävät niitä. Mahdollinen koulun vaihto ei aiheuta oppilaalle ongelmia.

Viisikulmiomallin mukaisesti käsitteiden ymmärtävä oppiminen pyritään varmistamaan kolmivaiheisella opetusmallilla (väline – kuva – symbolivaihe). Opettaja opettaa, ohjaa, arvioi oppimista ja antaa palautetta. Sekä oppilas että hänen vanhempansa saavat nopeasti tiedon mahdollisista heikoista oppimistuloksista. Tämä käynnistää lisäopetuksen hankkimisen ennen kuin oppilas on kokonaan ”pudonnut kärryiltä”.

Metakognitiivisia taitoja eli ajattelun ohjaamista ja oppimaan oppimista opetetaan ja harjoitellaan systemaattisesti ja tietoisesti. Strategioista keskustellaan ja niitä perustellaan.

Sekä opettaja että oppilaat arvostavat matematiikkaa, ongelmanratkaisua ja hyviä oppimistuloksia. Haastavien ongelmien ratkaiseminen vaatii työtä ja sinnikkyyttä, mutta oppilaat kokevat onnistumisen ongelmanratkaisussa palkitsevana. Helppous ja hauskuus eivät ole Aasiassa matematiikan opetuksessa keskeisiä asioita.

Singaporelainen opetusmenetelmä on monipuolinen, selkeä ja innostava. Samalla se on vaativa sekä oppilaalle että opettajalle. Se vaatii sitoutumista ja työntekoa. Se myös palkitsee työnteosta. Aasialaisen ajattelun mukaan on kunnia-asia menestyä koulussa saadakseen hyvän työpaikan ja onnistuakseen elämässään.

Kiitokset Hannu Korhoselle hyvistä kommenteista ja parannusideoista.

Aloituskuva Fahrul Azmi on Unsplash