Perushahmotusta neljännen ulottuvuuden mieltämiseen, osa 1 – Mitä ne ulottuvuudet ovat?
Matematiikan alkuperä on konkretiassa: lukumäärissä ja muussa ympäristön hahmottamisessa. Matematiikan voima ja kehityksen rajattomuuden takuu on abstrahoinnissa, käsítteiden yleistämisessä ja uuden luomisessa. Tuttuja arkipäivän asioita voidaan matematisoida ja toisaalta voidaan määritellä käsitteitä, joita emme pysty mieltämään arkikokemuksemme perusteella. Abstrakteja käsitteitä voi kuitenkin pyrkiä hahmottamaan hankkimalla kokemuksia, jotka auttavat liittämään uudet käsitteet entisestään tuttuihin. Tässä sarjassa tutustumme neljänteen ulottuvuuteen.
Sanomme omaa ympäristöämme kolmiulotteiseksi, koska voimme liikkua kolmeen suuntaan: kävellä eteen- tai taaksepäin, liikkua sivuaskelilla oikealle tai vasemmalle tai hypätä ylöspäin ja pudota takaisin alas. Pöydällä kävelevällä muurahaisella on vain kaksi suuntaa: eteen–taakse ja oikealle–vasemmalle. Sen maailma on siis kaksiulotteinen. Eikä sillä ole useampia ulottuvuuksia, vaikka alusta olisi kaarevakin kuten vesikuuppa tai skeittiramppi, koska se ei osaa hypätä irti pinnalta. Junan maailma on yksiulotteinen, koska suuntia on vain yksi: eteen–taakse.

Juna kulkee yhdessä ulottuvuudessa. Muurahaisella niitä on kaksi. Skeittaaja pääsee kolmanteenkin. [1]
Kolmeen ulottuvuuteen meidät sulkee oma havaintokykymme, mutta matematiikka voi vapauttaa meidät sen rajoituksista. On mahdollista kuvitella neljäs ja muitakin ulottuvuuksia. Niille ei ole nimeä, kun niistä keskustelemiseen ei vanhastaan ole ollut tarvetta. Englantilainen matemaatikko Charles Howard Hinton (1853–1907) kutsui kirjoituksissaan [2] neljännen ulottuvuuden suuntia kreikkalaisperäisillä nimillä ana ja kata. Seuraavassa yritämme tuoda esiin tilanteita, jotka auttaisivat hahmottamaan, mistä on kyse.
Geometriaa
Yksikertaisin matemaattinen olio on piste. Sen konkreettinen vastine on paikka avaruudessa. Piste itsessään on nollaulotteinen, sillä sen sisällä ei voi liikkua. Jos pistettä siirretään jonkin matkaa tiettyyn suuntaan, saadaan jana. Se on yksiulotteinen, sillä janalla oleva piste voi liikkua eteen ja taakse.
Kun janaa siirretään oma mittansa kohtisuoraan suuntaansa vastaan, saadaan neliö. Se on kaksiulotteinen, sillä sen sisällä oleva piste voi liikkua kahteen suuntaan. Kun neliö siirretään janan mitta kohtisuoraan tasoansa vastaan eli kolmannen ulottuvuuden suuntaan, saadaan kolmiulotteinen kappale: kuutio.
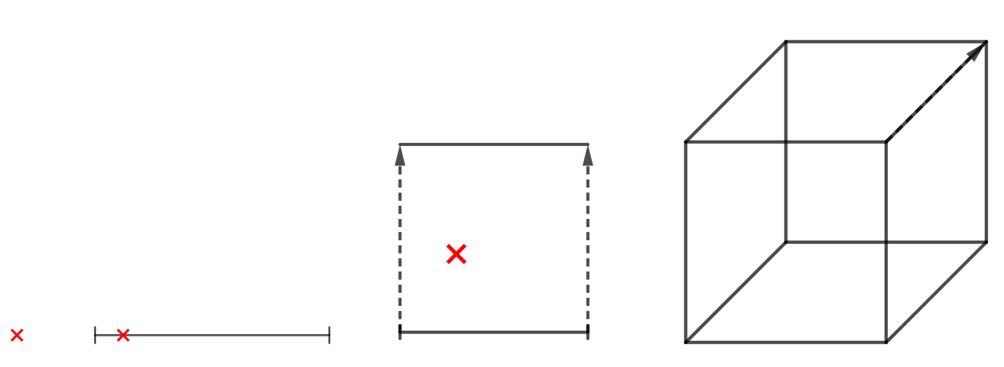
Pisteen laajentaminen kuutioksi yksi ulottuvuus kerrallaan.
Entä seuraava askel? Siirretään kuutio janan mitan verran kohtisuoraan kaikkia kolmea ulottuvuutta vastaan. Saadaan neliulotteinen kappale, jota nimitetään hyperkuutioksi tai tesseraktiksi. Kuvittelukykysi saattaa sotia vastaan. Jätetään mielikuvien muodostaminen sarjan myöhempiin osiin. Uskotaan, että sellainen kappale on olemassa. Millaisia ominaisuuksia sillä pitäisi olla?
Kun piste laajennetaan vaiheittain moniulotteiseksi objektiksi, niin kärkipisteiden lukumäärä muodostaa niin ilmeisen jonon (taulukko), että hyperkuutiolla täytyy olla 16 kärkipistettä. Tämä on tietysti selvää myös siksi, että alkuperäisellä kuutiolla on 8 kärkipistettä ja siirretyllä kuutiolla lisäksi 8. Viisiulotteisen ”kuution” kärkipisteiden määrä on ilmeisesti 32, mutta jätämme sen kappaleen tässä nimeämättä ja tutkimatta.
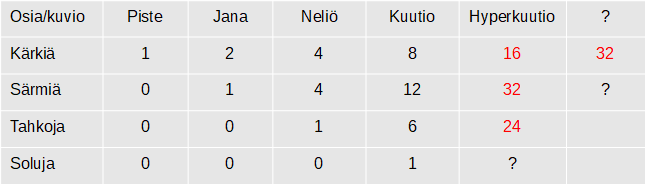
Monitahokkaan osien määrä kasvaa ja rakenne monimutkaistuu nopeasti ulottuvuuksien lisääntyessä. Kaikilla näillä on niin paljon yhteistä rakennetta, että janaa voitaisiin kutsua ”yksiulotteiseksi kuutioksi” ja neliötä ”kaksiulotteiseksi kuutioksi”
Janojen eli sivusärmien lukumäärän muodostumissääntökään ei ole kovin vaikea keksiä. Sääntö on ”lähtökuvion särmien määrä kaksinkertaisena ja kärkipisteiden määrä”. Kuution sivusärmien määräksi saadaan näin 12 ja hyperkuutiolle 32. Kuinka monta sivusärmää olisi vastaavasti viisiulotteisessa ”kuutiossa”? Perustele sääntö.
Neliöiden eli kaksiulotteisten sivutahkojen lukumäärän muodostumissääntö on jo ehkä vähän vaikeampi hahmottaa kuvasarjasta jo senkin takia, että jonosta ei näy kuin kaksi nollasta eroavaa jäsentä. Nyt on pakko kuvitella hyperkuution muodostumista. Lähtökuutiossa on 6 sivutahkoa ja siirretyssä kuutiossa samoin 6. Lisäksi tulevat siirtojanojen rajoittamat sivutahkot. Vastaus on 24, mutta jätämme säännön pohtimisen myöhemmäksi. Sääntö sinänsä on yhtä yksinkertainen kuin särmien lukumäärän muodostumissääntö.
Koordinaatistoja
Ulottuvuuksia voidaan yrittää hahmottaa myös koordinaatiston avulla. Kukin ulottuvuus tarvitsee oman toisista riippumattoman koordinaattiakselinsa. Piste ei tarvitse yhtään akselia. Yksiulotteisessa tapauksessa tarvitaan vain yksi suora (tai muu viiva), jota pitkin etäisyydet mitataan. Ennen vanhaan maanteiden varteen pystytettiin kilometripylväitä, jotka muodostivat ”tiekoordinaatiston” jakomerkit.
Kaksiulotteisella pinnalla tarvitaan paikan ilmoittamiseen kaksi koordinaattia ja siis kaksi koordinaattiakselia niin kuin koulumatematiikasta tutussa xy-koordinaatistossa on. Koordinaatistotason akselien voidaan kuvitella ulottuvan äärettömyyteen asti kummankin ulottuvuuden kummassakin suunnassa. Pallopinnalla tarvitaan paikan ilmoittamiseen myös kaksi koordinaattia: pallokartalla maantieteellinen pituus ja leveys. Tavallisesti akseleiksi ajatellaan päiväntasaaja ja Lontoon kautta kulkeva nollameridiaani.
Kolmen ulottuvuuden esittämiseen tarvitaan kolme akselia ja paikan ilmoittamiseen kolme lukua eli koordinaattia. Seuraavat ulottuvuudet on helppo ymmärtää vastaavalla tavalla. Neliulotteisen avaruuden kuvaamiseen tarvitaan neljä koordinaattia (x, y, z, w) ja niin edelleen. Koordinaatiston geometrinen hahmottaminen ei enää olekaan yhtä helppoa, mutta periaatteen pitäisi olla helposti ymmärrettävissä.
Neli- ja useampiulotteisiakin koordinaatistoja käytetään moniin tarkoituksiin. Eikä koordinaattien tarvitse tietenkään aina olla paikkakoordinaatteja. Suhteellisuusteorian yhteydessä on ollut esillä neliulotteiden avaruus–aika, kolme paikkakoordinaattia ja neljäntenä aika. Hiukkasfysiikan säieteorioissa on käytetty 9- ja jopa 26-ulotteisia malleja.
Fysiikan sana ”avaruus” on omaksuttu myös matemaattiseen käyttöön. Niinpä esimerkiksi kahden nopan heiton tuloksien joukkoa voitaisiin kutsua tulosavaruudeksi. Sen ”pisteet” ovat lukukaksikkoja, esimerkiksi (1, 3) ja (6, 6). Se avaruus on kaksiulotteinen: kuusi kertaa kuusi ‑ruudukko. Esimerkkinä kolmiulotteisesta avaruudesta voisi olla kolmiulotteinen teemakartta, jonka ulottuvuuksina ovat Tilastokoulun esimerkissä [3] puolueen kannatus eduskuntavaaleissa kunnittain sekä maantieteellinen pituus ja leveys.
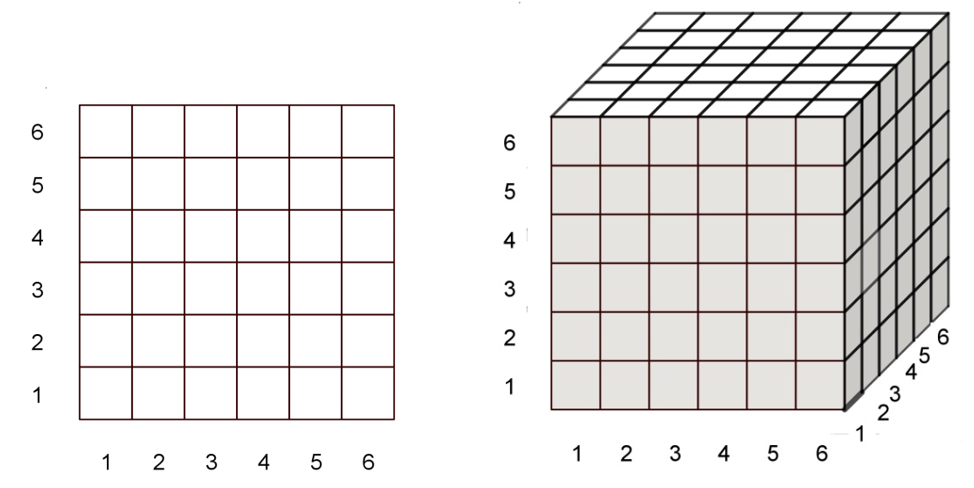
Vasemmanpuoleinen kuva esittää kahden nopan heiton tulosavaruutta. Ruutu (1, 1) kuvaa sitä, että kummallakin nopalla tuli ykkönen, ruutu (5, 2) sitä, että ensimmäisen nopan silmäluku oli 5 ja toisen 2. Mitä oikeanpuoleinen kuva voisi esittää?
Taulukoita
Mitä tahansa taulukkoa, johon on kirjattu muuttujien arvoja, voidaan ajatella tällaisena avaruutena. Sarakkeiden määrä kertoo tarvittavien ulottuvuuksien määrän ja sarakeotsikko kunkin ulottuvuuden nimen. Kullakin rivillä on yksi avaruuden ”piste”. Sen koordinaatit ovat rivillä oleva järjestetty arvojoukko. Tällainen avaruus ei ole yleensä ääretön, vaan siinä on vain äärellinen määrä pisteitä eli taulukon rivejä. Edellä olevassa kahden nopan heiton tulosavaruudessa on 36 pistettä. Taulukossa olisi siten kaksi saraketta ja otsikkorivin lisäksi 36 tapausriviä. Mitkä olisivat sarakeotsikot?
Tällaisia avaruuksia voit keksiä itsekin. Avaruuden ”pisteet” voivat olla esimerkiksi ihmisiä. Jos jokaisesta kirjataan neljä tietoa, esimerkiksi sukupuoli, pituus, paino ja ikä, niin syntyy nelisarakkeinen taulukko, joka voidaan myös mieltää neliulotteiseksi avaruudeksi. Mitkä olisivat sinun koordinaattisi tässä avaruudessa?
Sarja jatkuu.
[1] Juna: Kyle of Lochalsh, Skotlanti. Geograph.org.uk. CC BY-SA 2.0.
Muurahainen: kollaasi kamerakuvasta ja Geogebra-pallosta.
Skeittaaja: kuvaaja ei tiedossa, Creative Commons CC0.
[2] Hinton, C. H. A New Era of Thought. Swan, Sonenschein & Co, London 1888, osoitteessa
Katso myös Pickover, C. Surfing through Hyperspace. Oxford University Press, New York 1999, osoitteessa
[3] Tilastoteemakartat: Kolmiulotteinen teemakartta. Tilastokeskuksen tilastokoulu osoitteessa