Omaehtoista Geogebra-koulutusta
Opetus uusiutuu nopeasti. Opettajien tiedontarve on suuri. Pääkaupunkiseudun opettajat halusivat saada lisää Geogebra-koulutusta siitä huolimatta, että koulutusta on tarjolla muutenkin. Huutoon vastasi Suomen Geogebra-instituutti järjestämällä Geogebra-illan yhteistyössä Helsingin yliopiston kanssa.
Koulutuksen järjestämiseen on periaatteessa tarjolla paljon taloudellista tukea, mutta ad hoc -täsmäkoulutukseen sitä ei vain löytynyt. Helsingin yliopiston matematiikan, fysiikan ja kemian opettajan kandiohjelma tarjosi kuitenkin tilat ja MAOLin ja Suomalaisen Geogebra-verkoston kokeneet kouluttajat Terhi Korhonen, Lauri Hellsten, Hannu Mäkiö ja Mikko Rahikka toimivat opettajina vapaaehtoisesti. Mukana oli nelisen kymmentä Suomen Geogebra-verkoston postituslistan ja muun sosiaalisen median kautta tiedon saanutta opettajaa, pääosa pääkaupunkiseudulta, mutta myös kauempaakin sadan kilometrin säteeltä.
Illan näkökulma oli tieto- ja viestintätekniikan käyttö matematiikan oppimisessa ja opettamisessa, toteuttamisvälineenä Geogebra ja lähestymistapana matematiikassa, fysiikassa ja kemiassa opetettavat konkreettiset asiat. Lukion ryhmää sähköisti vielä erityisesti lähestyvä ylioppilaskirjoitusten matematiikankokeen digitalisoiminen. Käyttöyhteys on kuitenkin peruskoulussa ja lukiossa niin erilainen, että Geogebra-illan osallistujat työskentelivät kolmessa ryhmässä: peruskoulun matematiikka, lukion matematiikka ja fysiikka–kemia.
Suora keskustelu samojen ongelmien parissa painivien kollegojen kanssa on tietysti tällaisen vapaamuotoisen tilaisuuden parasta antia, mutta useita muitakin tarpeita tuli selvästi näkyviin. Ensiksikin materiaalia on niin paljon, että arkipäivän kiireissä ei jaksa kultajyviä etsiskellä; tarvitaan asiantuntevia kouluttajia valitsemaan. Toiseksi, vaikka Geogebran käytön aloittaminen on helppoa, ohjelma ja sen pedagoginen ympäristö ovat kasvaneet niin runsaiksi, että kaikkia toimintoja ei löydä kuin opastuksen avulla.
Kolmanneksi kouluttajat tekevät aina runsaasti materiaalia. Jos se luovutetaan julkisesti saataville niin kuin Geogebra-yhteisössä on ollut tapana alusta asti, niin tilaisuus ei jää vain mukana olleiden hyödyksi. Niin tehtiin tälläkin kerralla [1,2]. Samalla tuli esille myös MAOLin järjestämän täydennyskoulutussarjan julkisesti nähtävissä oleva materiaali [3]. Neljäntenä ja tärkeimpänä on kuitenkin opetuksessa jo kokeiltujen materiaalien pedagogisen tarpeen, annin ja merkityksen pohdiskelu.
Yläkoulu
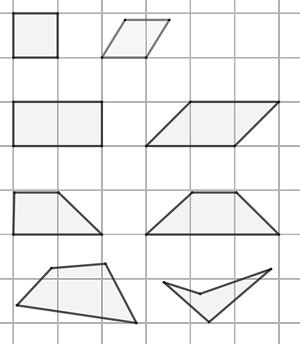
Yläkoulun ryhmässä todettiin, että oppilaat omaksuvat Geogebran peruskäytön nopeasti. Eikä kyse ole vain Geogebrasta, vaan samalla välittyy yleisemminkin sähköisten työvälineiden käyttöön liittyviä ajattelu- ja toimintatapoja. Vaikka aloittaminen on helppoa, niin koko ohjelman haltuunotto vie aikaa. Hitauden hyväksymistä helpottaa viiden askeleen malli: tee kuvia kokeisiin, havainnollista oppitunnilla, anna opastettuja tehtäviä oppilaille, käytä ja anna oppilaiden käyttää työvälineenä tarpeen mukaan sekä omaksu ajattelun ja ongelmanratkaisun välineeksi. Ehkä lukukausi kerrallaan, siis kahden ja puolen vuoden oppimisprosessi opettajalle ennen kuin väline on hyvin hallussa, vaiheita limittämällä ehkä puolitoista vuotta. Samat vaiheet ovat käytännössä edessä oppilaalla, vaikka prosessin onkin heidän kohdallaan edettävä paljon nopeammin.
Nykyiset opetussuunnitelman perusteet velvoittavat Geogebran tai jonkun muun vastaavan ohjelmiston käyttämiseen matematiikan oppimisen osana. Yläkoulun matematiikan tavoitteissa mainitaan erityisesti taulukkolaskenta ja (jokin) dynaaminen geometriaohjelma ja laaja-alaisen osaamisen tavoitteissa vielä tieto- ja viestintäteknologian käyttö- ja toimintaperiaatteet ja keskeiset käsitteet. Päämäärään päästään tietysti käyttämällä monia laitteita ja ohjelmistoja, mutta syvällisempiä vaikutuksia sekä ajattelussa että toiminnassa voidaan odottaa vasta sitten, kun yksi työväline tulee niin tutuksi, että siitä tulee luonteva ja luotettava työskentelyn väline, vaihe viisi edellä.
Geogebra on monipuolisuutensa ansiosta kelpo valinta siksi, että se sisältää työvälineet kaikille keskeisille perusopetuksen matematiikan osa-alueille: luvut ja laskutoimitukset, algebra, funktiot, geometria sekä tilastot ja todennäköisyys. Ehkä eniten Geogebra helpottaa funktioiden kanssa työskentelemistä, kun kuvaaja ilmestyy näkyviin heti, kun lauseke saadaan kirjoitetuksi syöttökenttään. Se on sitten muunneltavissa dynaamisesti ilman, että olisi tarpeen piirtää uutta kuvaajaa. Geogebra sisältää myös taulukkolaskennan, CAS-laskimen ja tilastotoimintoja. Geogebran kielioppia on helpompi ymmärtää, jos mieltää komennot funktioiksi, merkintä $f(x)$, ja muistaa, että argumenttina voi olla esimerkiksi hyvinkin monialkioinen lista. Tämän yhteyden tiedostaen Geogebran komentojen käyttö on funktionaalista ohjelmointia, vaikkakin komento kerrallaan.
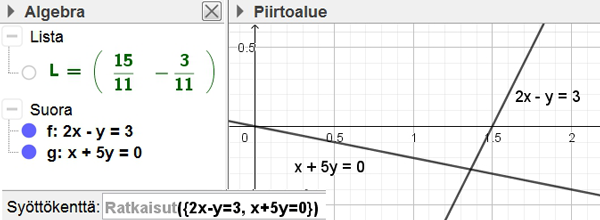
Lukio
Geogebran käytössä ja digitalisoitumisessa on kaksi puolta. Yhtäältä on kyse oppimistulosten arvioinnista. Mitä tietovälineitä tai ohjelmia kokeissa saa käyttää ja millä ohjelmilla koetehtävien vastaukset annetaan. Lukiossa tätä ohjaavat ylioppilaskirjoitusten sähköistyminen ja opetussuunnitelman perusteiden kurssikohtaisten kuvailujen tekstit. Matematiikka on ilmeisesti erityisen hankala, sillä lähes puolet ylioppilaskirjoitusjärjestelmään sisällytetyistä ohjelmista ovat matematiikan erityisohjelmia. Geogebra on yksi näistä.
Toisaalta ja ehkä tärkeämpänä on digitalisoimisen vaikutus opetukseen, opiskeluun ja oppimiseen. Lukiossa laite-edellytykset ovat kunnossa, sillä lähes kaikilla oppilailla on käytössään tabletti tai kannettava tietokone. Ohjelmistojen osalta tilanne on paljon kirjavampi, mitä osoittaa jo ylioppilaskirjoitusjärjestelmään otettujen matematiikkaohjelmien määrä. Ehkä matematiikassa olisikin hyvä suuntautua vähitellen irrallisista ohjelmista monipuolisten oppimisympäristöjen kuten Geogebran suuntaan ja parhaimmillaan toimia niin, että väline olisi tuttu jo perusopetuksesta.
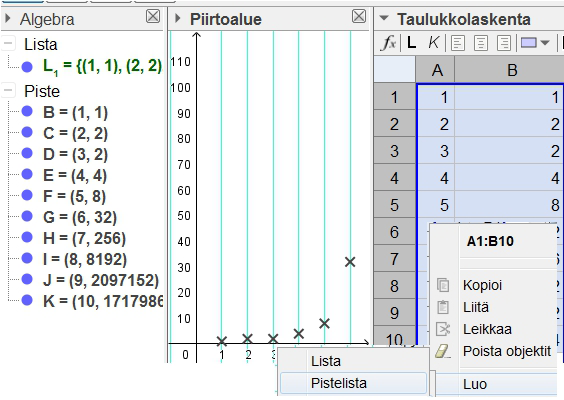
Geogebra-illan lukioryhmässä ei tällaisia yleisiä näkökohtia pohdittu, vaan keskityttiin opetussuunnitelman perusteiden mukaisiin tavoitteisiin ja sisältöihin liittyvien toimintojen opettelemiseen. Jo ensimmäisessä yhteisessä kurssissa on aiheita, joissa joihin tutustumisessa ja joiden havainnollistamisessa matematiikkaohjelmistoista on olennaista apua. Esimerkiksi [2] lukujonojen käsittelyyn Geogebra tarjoaa kaksi erilaista työvälinettä: taulukkolaskennan ja Jono-komennon. Taulukkolaskennan käyttö sopii erityisesti rekursiivisten jonojen rakenteluun ja mittaustulosten käsittelyyn fysiikassa ja kemiassa. Jos taulukkolaskenta on jo tuttu, niin se ei vaadi Geogebrassa mitään uutta opeteltavaa.
Tietotekniikka on tullut opetussuunnitelman perusteisiin ja ainakin ylioppilaskirjoitusten matematiikan kokeeseen selvästi tekniikka edellä. Kovasti kaivattaisiin syvällisempää pohdiskelua matematiikan opetuksen päämääristä ja opettamisen tavoista. Välineet hoitavat laskemisen ja piirtämisen suurelta osalta. Aikaa pitäisi siis säästyä sekä ajatteluun että keksivään ja tutkivaan oppimiseen. Onko kuitenkin niin, että edelleen pidetään käsin laskemisen rutiineita niin tärkeinä, että niitä testataan kokeissa, varsinkin kaksiosaisen kokeen ensimmäisessä osassa. Eikö myös arvioinnin pitäisi muuttua opetuksen muuttuessa. Nyt on puolin ja toisin vielä ilmeisen epäselvää, mikä on tavoiteltava käsinlaskemisen taso.
Opiskelija tarvitsee aikaa myös välineen oppimiseen. Tämä aika on poissa matematiikan oppimisesta, olkoonkin että suuri osa siitä käytettiin ennen ja käytetään ehkä vielä nykyäänkin rutiininomaisten laskutoimitusten automatisoimiseen. Ehkä tämä aika olisikin käytettävä Geogebran käytön oppimiseen, vastaavathan sen laskenta- ja piirtämistoiminnot juuri samoihin apuvälinetarpeisiin kuin rutiininomaisiksi harjoitellut lasku- ja piirtämistaidot. Vasta hyvin haltuun saatu työväline tukee ja ohjaa ajattelua ja ongelmanratkaisua niin tehokkaalla tavalla kuin instrumental genesis -ajattelusta saadut kokemukset osoittavat.
Opettajalla on suuri vastuu siinä, mille tasolle opiskelijan Geogebra-osaaminen pitäisi viedä. Opetussuunnitelma-asiakirjat eivät opasta tässä. Luontevaa kuitenkin olisi, että GeoGebrasta tulisi opiskelijallekin työväline ongelmien ratkaisemiseen ja tilanteiden mallintamiseen eikä se jäisi vain muistinvaraisesti opittujen toimintojen mekaaniseen käyttöön. Minimitavoite voisi olla se, että opiskelija hallitsee sekä piirtoalueen että algebra- ja CAS-ikkunan useimmin tarvittavat toiminnot ja muutaman peruskomennon. Syvällisempi osaaminen avaa tietysti aivan uusia mahdollisuuksia matematiikan tekemiseen, erityisesti mallintamiseen. Opettajan tehtäväksi jää päättää viime kädessä, kuinka paljon oppilaan on osattava.
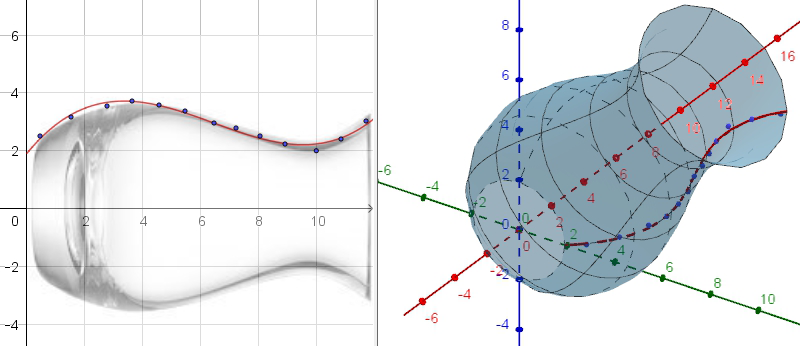
Oppimisen kannalta Geogebra on välistä liian nopea, kun tekeminen on niin helppoa. Esittävän opetuksen ja oppilastehtävien tulisi olla sellaisia, että opiskelija ehtii ja joutuu pohtimaan. Tärkeintä ei lopultakaan ole se, miltä lopputulos näyttää, vaan millaisia ajatteluprosesseja opiskelija on käynyt läpi. Excel-taulukkolaskentaa ja kuvaajanpiirto-ohjelmia lukuun ottamatta ei matemaattisille aineille ole näihin asti juurikaan ollut pedagogisesti järkeviä ohjelmia. GeoGebra tai sen kaltainen muu laaja-alainen matematiikan oppimiseen suunniteltu oppimisympäristö muuttaa tilanteen täysin. Ero on ehkä vielä suurempi luonnontieteissä kuin matematiikassa, sillä mittaustulosten käsittely, kuvaajien piirto ja käyrien sovittaminen sujuvat nopeasti ja aikaa voidaan käyttää ilmiöiden ja sovellusten tarkasteluun.
Illan päätteeksi monet kyselivät, milloin vastaava ilta toteutettaisiin heidän paikkakunnallaan. Monet kerhot ovat niin jo tehneetkin. Reippaasti vain tekemään. Illan materiaalit ovat vapaasti käytettävissä. Tarvittaessa voi neuvotella asiasta Geogebra-instituutin kanssa ja kysellä, miten verkoston toimintaan pääsee mukaan. Ota yhteyttä geogebra.fi-sivuston kautta tai suoraan sähköpostilla geogebra(at)hyl.fi. Verkoston ideanahan on ”opettajilta opettajille”.
Viitteet
[1] Yläkoulun materiaalit osoitteessa http://51.fi/Geogebra_18042018, viitattu 20.4.2018
[2] Lukion materiaalit osoitteessa bit.ly/GG42018, viitattu 20.4.2018.
[3] Yläkoulun materiaalit: ”Ohjelmistojen pedagoginen hyödyntäminen matematiikassa, fysiikassa ja kemiassa”. Linkit osoitteessa: https://maol.fi/materiaalit/ohjelmistojen-pedagoginen-hyodyntaminen-matematiikassa-fysiikassa-ja-kemiassa/
Lukion materiaalit: ”Digitaalisten aineistojen pedagoginen hyödyntäminen matematiikassa, fysiikassa ja kemiassa” linkissä https://maol.fi/materiaalit/materiaalit/.