Matematiikan lukio- ja ylioppilastutkintoarvosanat – Selittääkö heikko arvosanataso lyhyen matematiikan kokeen jättämisen pois tutkinnosta?
Ylioppilastutkinnon painoarvon kasvattaminen yliopistojen opiskelijavalinnassa on puhuttanut viime aikoina niin opiskelijoita, lukio- ja yliopistoväkeä kuin laajempaa yleisöä (esim. Yle, 2019). Keskustelun ytimessä on ollut ylioppilastutkinnon ja pääsykokeiden vastakkainasettelu, mutta myös pitkän matematiikan perusteettomaksi koettu asema etenkin ”ei-matemaattisten” alojen opiskelijavalinnassa. Artikkelimme pääpaino on pitkän ja lyhyen matematiikan lukioarvosanoissa sekä niiden yhteydessä vastaaviin ylioppilastutkinnon matematiikan kokeen arvosanoihin. Sivuamme kuitenkin myös tätä pitkän matematiikan opiskelijavalinnassa tuomaa suurta pistesaalista.
Ylioppilastutkinnon arvosanat osaamisen mittarina
Ylioppilastutkinnon yksittäiset kokeet ennustavat hyvin niin opiskelijoiden menestystä tutkinnon muissa kokeissa kuin heidän menestystään myöhemmissä opinnoissaan (Kupiainen, Marjanen & Ouakrim-Soivio, 2018). Ennustavuudessa on kuitenkin selviä oppiainekohtaisia eroja, jotka on keväästä 2014 lähtien huomioitu ylioppilastutkinnon arvosanajakaumissa (nk. SYK eli standardisoitujen yhteispisteiden keskiarvo) ja keväästä 2019 lähtien korkea-asteen opiskelijavalinnan pisteytysmallissa. Pitkän matematiikan tuomaa muita oppiaineita suurempaa pistesaalista voidaan siis tutkimuksen valossa pitää oikeutettuna. Tämä ei kuitenkaan tarkoita, että pisteytys olisi toteutuneessa muodossaan kaikin puolin onnistunut (esim. Kupiainen, 2019).
Lukio- ja ylioppilastutkintomenestyksen välinen yhteys
Ylioppilastutkinnon arvosanoihin keskeisesti kietoutuva mutta vähemmän tutkittu kysymys on niiden yhteys opiskelijoiden lukioaikaiseen menestykseen kyseisessä oppiaineessa. Uudempi tutkimuksemme (Kupiainen & Ouakrim-Soivio, 2019) kuitenkin osoittaa, että ylioppilastutkinnon kaikki kokeet mittaavat opiskelijoiden menestystä kyseisessä oppiaineessa lukion ensimmäisestä kurssista viimeiseen jopa hämmästyttävän hyvin. Laudaturin kirjoittajat ovat saaneet joka ainoasta kurssistaan keskimäärin paremman arvosanan kuin eximian saaneet, jotka taas ovat saanet paremman kuin magnan kirjoittajat jne. approbaturiin asti. Vain improbatur muodostaa tähän pienen poikkeuksen paljastaen, että epäonnistumiseen voi todellakin olla monia syitä heikosta viime hetken valmentautumisesta aitoon heikkoon osaamiseen.
Vaikka yhteys on keskiarvon tasolla vahva, siihen sisältyy huomattavaa lukiokohtaista vaihtelua. Lukioarvosanojen käyttö ilman kaikille yhteistä (joskin koevalintojen pirstomaa) ylioppilastutkintoa asettaisi siis hakijat eriarvoiseen asemaan tavalla, joka muistuttaisi tilannetta, joka vallitsee täällä hetkellä perusopetuksen päättyessä.
Tutkimusaineisto
Tutkimuksemme on osa laajempaa kokonaisuutta, jossa on seurattu metropolialueen 14 kunnan yhden ikäluokan osaamisen ja hyvinvoinnin kehitystä seitsemännen luokan alusta syksyllä 2011 toisen asteen loppuun (Hotulainen ym., 2016). Kohdejoukkona ovat ne aineiston 6 179 lukiolaista, jotka aloittivat lukion välittömästi peruskoulun jälkeen syksyllä 2014 ja saivat valkolakkinsa keväällä 2017*. Kurssiarvosanat on saatu lukioista ja ylioppilastutkintoarvosanat ylioppilastutkintolautakunnasta. Tutkimus on kokonaisuudessaan THL:n eettisen lautakunnan hyväksymä. Alueellisesta rajoittuneisuudestaan huolimatta aineisto edustaa siis yli viidesosaa kevään 2017 ylioppilaista. Matematiikan arvosanojen osalta on huomioitava, että opiskelijat aloittivat siis lukio-opintonsa ennen vuoden 2015 opetussuunnitelman mukaista MAY1-kurssia (ks. Eronen, Portaankorva-Koivisto, Kupiainen & Hannula, 2017; Portaankorva-Koivisto, Eronen, Kupiainen & Hannula, 2017).
* Aineistosta puuttuvat siis opiskelijat, jotka eivät suorittaneet tutkintoaan kolmessa vuodessa sekä teknisen virheen vuoksi neljän helsinkiläislukion ja yhden kehyskunnan lukion kevään 2017 ylioppilaat.
Lukion kurssiarvosanat
Lukioarvosanojen ja ylioppilastutkintoarvosanojen suoraa vertailua vaikeuttavat sekä oppiaineiden väliset erot arvosanoissa että erot eri kokeita tutkintoonsa valitsevien opiskelijoiden osuudessa ja keskimääräisessä osaamisen tasossa (Taulukko 1).
Taulukko 1. Lukion pakollisten ja syventävien kurssien arvosanat ja kurssimäärät oppiaineittain sekä kyseisen kokeen kirjoittaneiden määrä ja keskimääräinen arvosana kirjoittamissaan kokeissa (Ka). Taulukosta on jätetty pois C-kielet sekä ne oppiaineet, joiden kirjoittajia oli aineistossa vähemmän kuin 50.
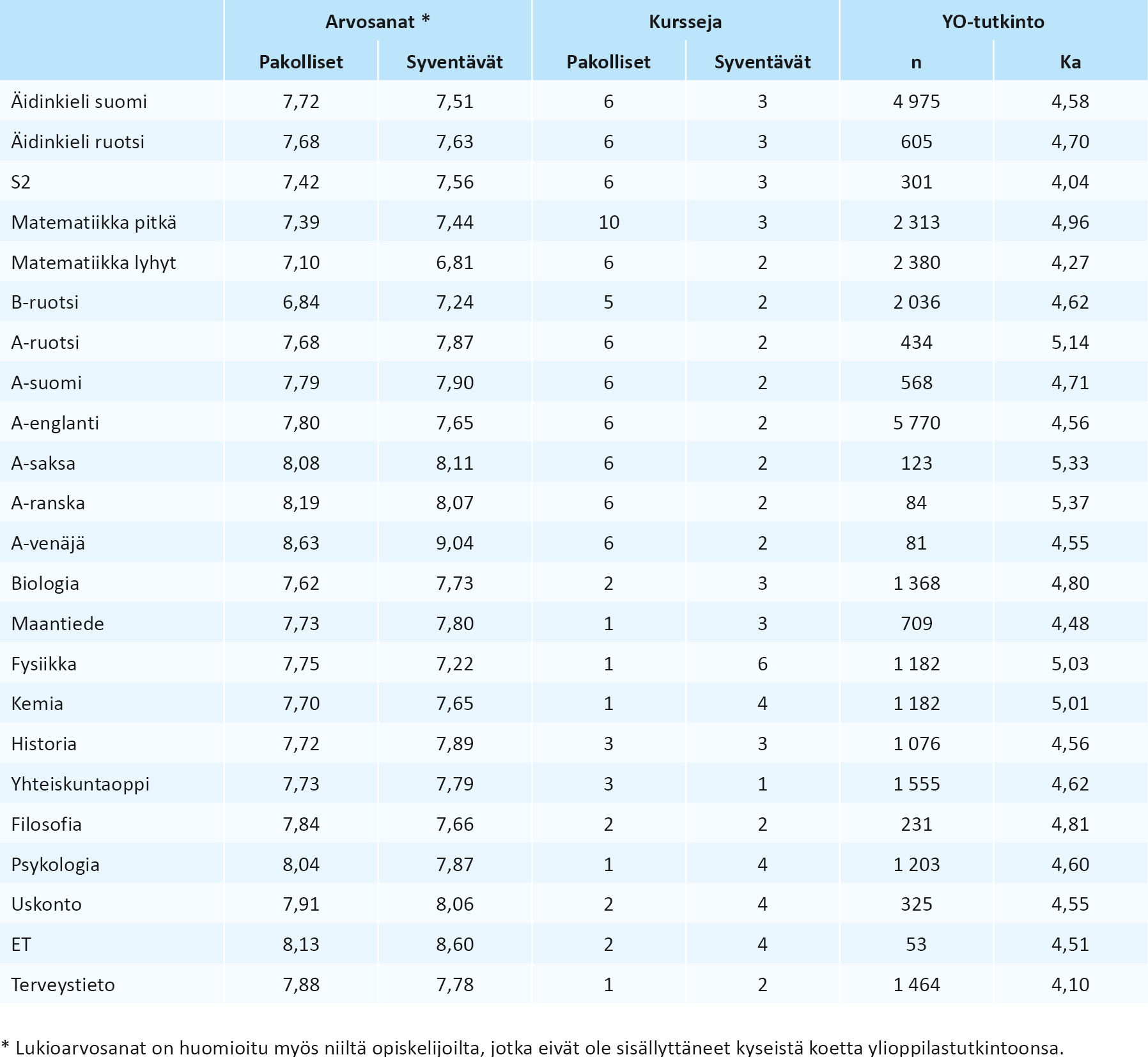
Kuten Taulukosta 1 voidaan nähdä, oppiaineiden välillä on huomattavia eroja niin pakollisten ja syventävien oppiaineiden keskimääräisessä arvosanatasossa kuin opiskelijoiden keskimääräisessä ylioppilastutkintomenestyksessä. Matematiikka ja B-ruotsi erottuvat muista oppiaineista niitä alhaisemmalla arvosanatasollaan, kun taas lyhyt matematiikka eroaa pitkästä matematiikasta siinä, että sen arvosanojen keskiarvo laskee selvästi opiskelijoiden opintojen edetessä. Osin kyse voi olla opiskelijoista, jotka ovat päättäneet jo ehkä ennen lukioon tuloa jättää matematiikan kirjoittamatta, osin opiskelijoiden heikoista matematiikan perustaidoista (ks. Metsämuuronen & Tuohilampi, 2017). Sama arvosanojen selvä heikkeneminen opintojen edetessä on havaittavissa myös fysiikassa.
Matematiikan kurssi- ja ylioppilastutkintoarvosanat
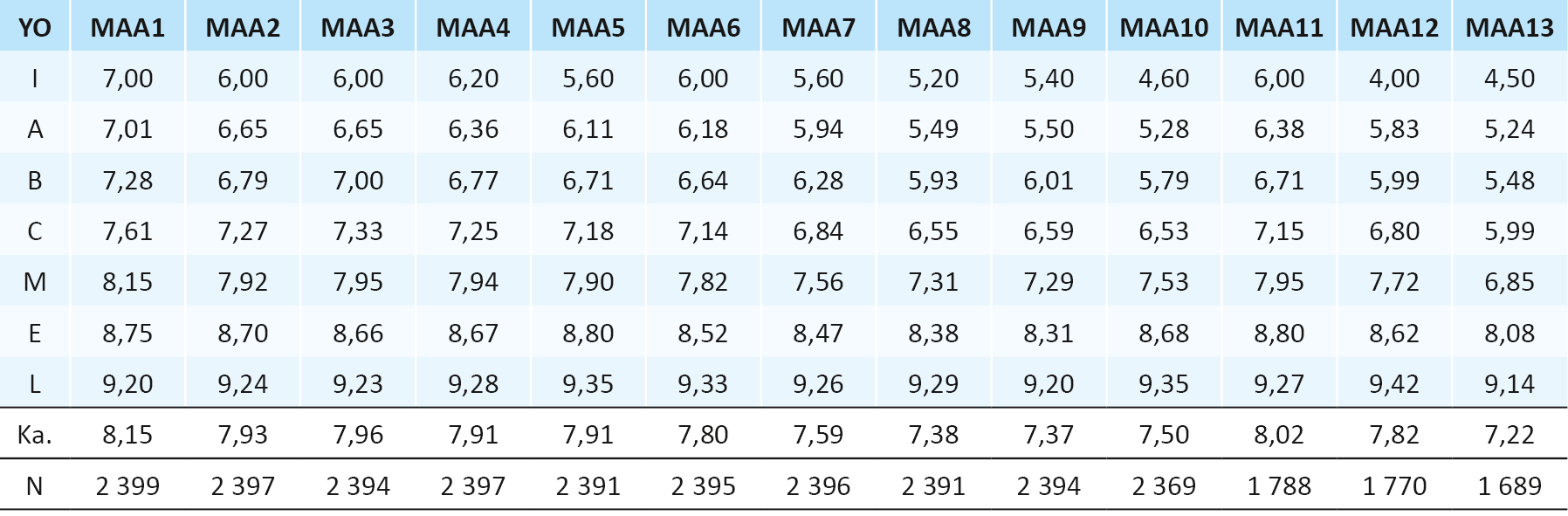
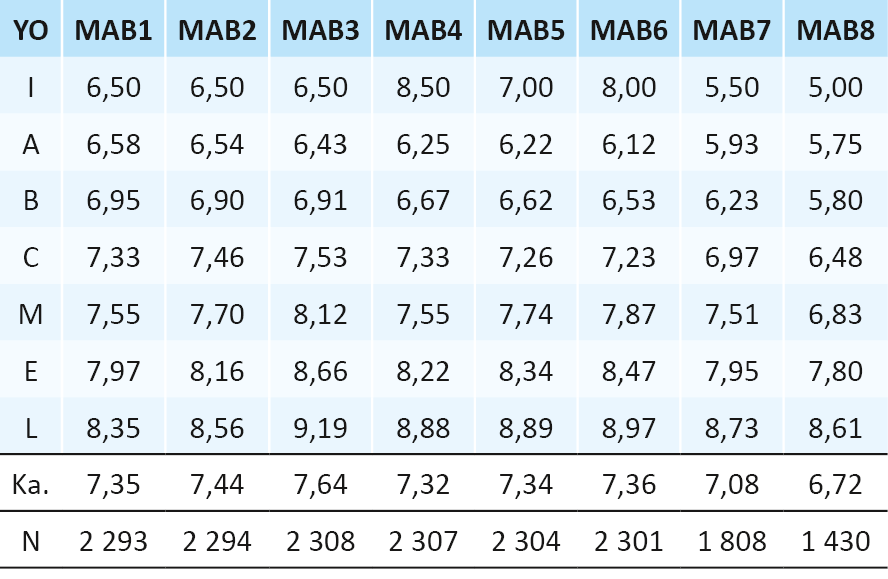
Edellä jo mainittu lukio- ja ylioppilastutkintokokeiden arvosanojen välinen yhteys oli selvä myös matematiikassa. Taulukossa 1 nähty ero pitkän ja lyhyen matematiikan kurssiarvosanoissa korostuu kuitenkin entisestään, kun kurssiarvosanoja verrataan ylioppilastutkinnon arvosanoihin (Taulukko 2 ja Taulukko 3).
Taulukko 2. Pitkän matematiikan kurssikohtaiset arvosanakeskiarvot ylioppilastutkinnon koearvosanan (YO) mukaan.
Taulukko 3. Lyhyen matematiikan kurssikohtaiset arvosanakeskiarvot ylioppilastutkinnon koearvosanan (YO) mukaan.
Taulukko 4. Lyhyen matematiikan kirjoittajien pitkän matematiikan kurssien arvosanakeskiarvot ylioppilastutkinnon koearvosanan (YO) mukaan.

Kuten taulukoista 2 ja 3 voidaan nähdä, sekä lyhyen että pitkän matematiikan kirjoittajien ylioppilastutkintoarvosanat heijastavat varsin systemaattisesti heidän menestystään läpi lukiokurssien. Arvosanoissa on kuitenkin odotusten vastaiselta näyttävä ero. Koska enemmistö matematiikan tutkinnostaan pois jättävistä on lyhyen matematiikan lukijoita, kirjoittajien lukioaikaisten arvosanojen olettaisi olevan pitkän matematiikan kirjoittajia korkeampia, ovathan he selvästi valikoituneempi osa kyseisen oppimäärän opiskelijoista. Pitkän matematiikan kurssiarvosanat olivat ylioppilastutkinnon näkökulmasta tarkasteltuna lähellä tasoa, jolla ne olivat muissa oppiaineissa eli pitkästä matematiikasta laudaturin saaneiden ylioppilaiden kurssiarvosanojen keskiarvo oli 9,27, kun se oli esimerkiksi A-englannissa 9,28, historiassa 9,42 ja psykologiassa 9,47. Lyhyestä matematiikasta laudaturin saaneiden kurssiarvosanojen keskiarvo oli sen sijaan vain 8,77. Myös pitkän ja lyhyen matematiikan arvosanajakaumat erosivat ainakin tässä aineistossa selvästi toisistaan (Kuva 1).
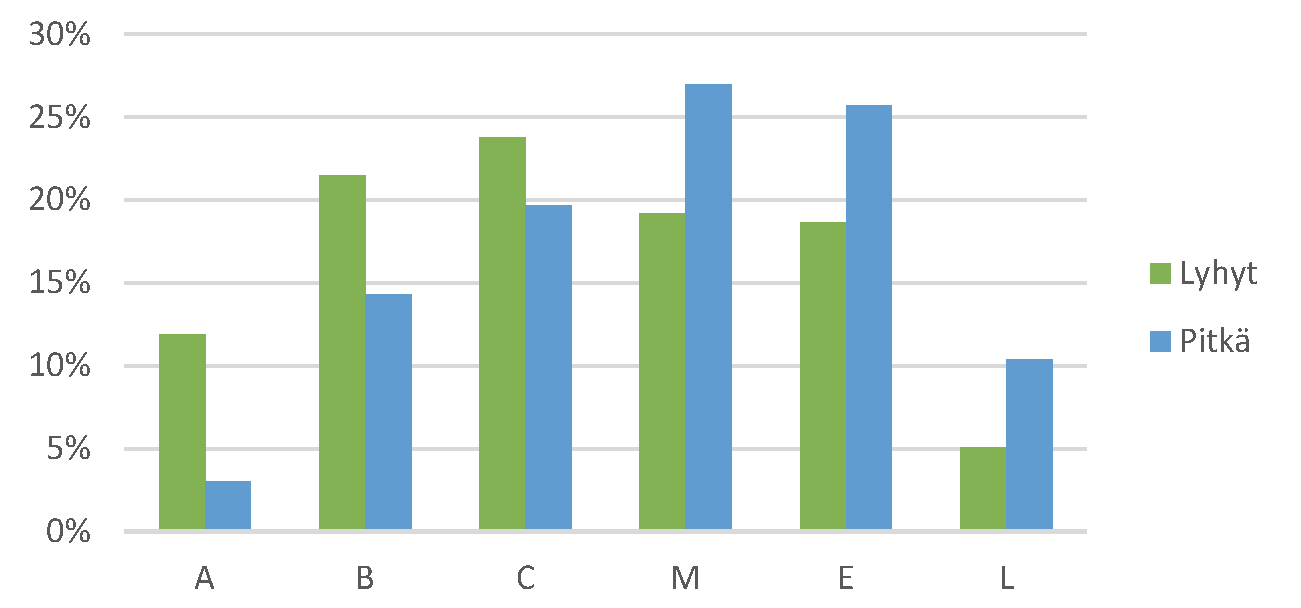
On kuitenkin huomattava, että Taulukossa 3 on kyse nimenomaan lyhyen matematiikan kurssien arvosanoista. Lyhyen matematiikan kirjoittajista 472 (19�
Pitkää matematiikkaa pidemmällekään lukeneiden keskimääräinen kurssimenestys ei olisi keskimäärin yltänyt pitkässä matematiikassa edes approbaturiin, ja laudaturin saaneidenkin pitkän matematiikan kurssiarvosanojen keskiarvo oli 6,66, mikä olisi pitkässä matematiikassa yltänyt keskimäärin arvosanaan B tai C. Pitkää matematiikkaa vähintään yhden kurssin opiskelleiden osuus oli kuitenkin lyhyen matematiikan laudaturin kirjoittajista peräti 34 prosenttia ja he veivät myös 27 prosenttia eximia-arvosanoista (M 22�
Pohdinta
Tutkimuksen tulokset tukevat kokonaisuudessaan Kupiaisen ja kollegojen aiemman laajan ylioppilastutkintoa koskevan tutkimuksen (2018) tuloksia eli osoittavat lukiolaisten jakautuvan selvästi kolmeen ryhmään ylioppilastutkintoon sisällytetyn tai ei-sisällytetyn matematiikan kokeen mukaan. Tulokset tukevat myös Kupiaisen ja Hotulaisen aiempaa samaan metropolialueen nuorten aineistoon perustuvaa havaintoa (2018) pitkästä matematiikasta lyhyeen vaihtaneiden pienestä lisäryhmästä.
Vertailu pitkän ja lyhyen matematiikan lukio- ja ylioppilastutkintoarvosanojen välillä herättää kuitenkin kysymyksiä. Onko lyhyen matematiikan opiskelijoiden osaamisen taso todellakin niin paljon alhaisempi suhteessa LOPS:in vaatimuksiin kuin pitkän matematiikan lukijoiden, että se oikeuttaa eron arvosanojen ja ylioppilaskokeen tulosten välisessä suhteessa myös parhaiten osaavilla? Muutaman vuoden takainen KARVI:n matematiikan oppimistulosten arviointi osoitti, että näin on ainakin vähiten matematiikkaa opiskelleilla eli monen opiskelijan matematiikan taidot eivät kehity lukion aikana lainkaan siitä, mihin ne peruskoulun päättyessä jäivät (Metsämuuronen, 2017). Entä jos nykyisen kaltainen ’vapaaehtoinen’ heikko suoriutuminen ei olisi mahdollista ja matematiikan kokeesta tehtäisi äidinkielen tavoin pakollinen? Matematiikka, äidinkieli ja vieras kieli voisivat tulla tällöin huomioiduksi korkea-asteen opiskelijavalinnassa yleisenä jatko-opintovalmiuskokonaisuutena, joka poistaisi pitkän matematiikan tällä hetkellä ongelmalliseksi koetun aseman muiden oppiaineiden rinnalla.
On syy lyhyen matematiikan alhaiseen arvosanatasoon mikä hyvänsä, on kysyttävä, mikä vaikutus sillä on lyhyen matematiikan lukijoiden valmiuteen valita koe ylioppilastutkintoonsa. Kuinka moni opiskelija, jonka kurssiarvosanojen keskiarvo jää selvästi alle yhdeksän, voisi arvata, että hän voi pienellä loppukirillä saada osaamisellaan lyhyestä matematiikastaan laudaturin – etenkin, kun viidakkorumpu varoittaa pitkän matematiikan lukijoiden vievän sen hänen nenänsä edestä? Etenkin monen taitojaan epäilevän tytön valinta voi helposti osua vaihtoehtona olevaan B-ruotsiin, vaikka myös siinä pitkän matematiikan kirjoittajien arvosanat nousevat keskimäärin muita korkeammiksi.
Lähteet
Eronen, L., Portaankorva-Koivisto, P., Kupiainen, S., & Hannula, M. (2017). Lukion opiskelijoiden ja opettajien ensikokemuksia matematiikan yhteisestä MAY-kurssista. Dimensio, 81(4), 31-37.
Hotulainen, R., Rimpelä, A., Hautamäki, J., Karvonen, S., Kinnunen, J.M., Kupiainen, S., Lindfors, P., Minkkinen, J., Pere, L., Thuneberg, H., Vainikainen, M.-P., Wallenius T. (2016) Osaaminen ja hyvinvointi yläkoulusta toiselle asteelle Tutkimus metropolialueen nuorista. Helsingin yliopisto, Käyttäytymistieteellinen tiedekunta. Opettajankoulutuslaitos. Tutkimuksia 398.
Kupiainen, S. (2019). On taas se aika vuodesta … Ylioppilastutkinto ja korkeakouluvalinta.
Kupiainen, S. & Hotulainen, R. (2016). Girls, boys and STEM revisited: The role of grades guiding students’ educational choices in Finnish secondary education. Paper presented in EARLI Sig 18 & 23, Oslo, Norway, September 2016. Julkaisematon käsikirjoitus.
Kupiainen, S., Marjanen, J. & Ouakrim-Soivio, N. (2018). Ylioppilas valintojen pyörteessä. Suomen ainedidaktisen tutkimusseuran julkaisuja. Ainedidaktisia tutkimuksia 14.
Kupiainen, S. & Ouakrim-Soivio, N. (2019). Do centralised upper secondary school exit examinations offer added value? Paper presented in NOFA7-conference in Stockholm, 13.–15.5.2019. Julkaisematon käsikirjoitus.
Metsämuuronen, J. (2017). Oppia ikä kaikki–Matemaattinen osaaminen toisen asteen koulutuksen lopussa 2015. Helsinki: Kansallinen koulutuksen arviointikeskus. Julkaisut, 1, 2017.
Portaankorva-Koivisto, P., Eronen, L., Hannula, M. S., & Kupiainen, S. (2018). Lukion ensimmäinen yhteinen matematiikan kurssi–mielekästä ja merkityksellistä? FMSERA Journal.
Yle (2019). Ristola, P. & Jansson, K.: Syökö pitkän matematiikan suosio yleissivistystä? Yle kysyi rehtoreilta – ”Opiskelijoiden jaksaminen on heikentynyt ja taito- sekä taideaineiden opiskelu on vähentynyt”. Yle. Uutiset.







