Lukiolaisten perustelutaitojen parantaminen lämpöopissa MAOL-LUMA-yhteistyönä
Lukion opetussuunnitelman perusteet ja elokuussa voimaan astuva uusi lukiolaki kannustavat opettajia entistä tiiviimpään yhteistyöhön koulun ulkopuolisten tahojen kanssa [1,2]. Matemaattisten Aineiden Opettajien Liitto MAOL ry ja LUMA SUOMI -verkosto ovat luontevia opettajien yhteistyökumppaneita, sillä ne tarjoavat monipuolisia mahdollisuuksia opetuksen kehittämiseen. Tässä artikkelissa kuvataan näiden tahojen kautta toteutunut yhteistyö, jonka tuloksena suunniteltiin ja toteutettiin lukiolaisten perustelutaitojen kehittymistä tukeva lämpöopin opetuskokonaisuus. Kokonaisuuden materiaalit jaetaan artikkelin yhteydessä kaikkien opettajien vapaaseen käyttöön.
Yhteistyön kuvaus
Itä-Suomen yliopiston LUMA-keskus järjesti Joensuussa MAOL:n syyspäivillä 2018 argumentointia painottavan luonnontieteiden kouluopetuksen työpajan. Työpajassa käsiteltiin luonnontieteille ominaista argumentointia ja työtapoja, joiden avulla argumentointia voidaan painottaa luonnontieteiden kouluopetuksessa [3]. Työpajan päätteeksi opettajilla oli mahdollisuus kokeilla argumentoinnin painottamista omassa opetustyössään yhteistyössä työpajan vetäjän (Mikko Kesonen) kanssa. Yhteistyön tarkoituksena oli tarjota opettajille mahdollisuus kehittää heidän opetustarpeisiinsa soveltuva argumentointia painottava opetuskokeilu. Fysiikan ja matematiikan opettaja Riitta Salmenoja Loimaan lukiosta hyödynsi yhteistyömahdollisuuden, minkä tuloksena syntyi argumentointiharjoitus lämpöopin FY2-kurssille.
Argumentointiharjoitus tehtävineen
Harjoituksen aiheeksi valittiin lämpöoppi, koska sitä käsitellään ensimmäisellä fysiikan valinnaisella lukiokurssilla, jonka aikana fysiikalle ominaisten perustelu- ja argumentointitaitojen harjoittelu on tärkeää. Opetuskokeilun tavoitteena oli tukea lukiolaisten taitoja perustella laskennallisten tehtävien vastauksia, jotta niistä välittyisi looginen, fysiikan sisältötietoon ristiriidattomasti nojautuva ja hyvin perusteltu ratkaisu pelkän kaavaan sijoituksen sijaan.
Lämpöopin tehtävä argumentoinnin painottamiseksi
Opettaja hyödynsi harjoituksen suunnittelussa argumentointia painottavaa lämpöopin tehtäväkokonaisuutta [4], joka on kehitetty Itä-Suomen yliopiston LUMA-keskuksessa. Yläkouluun tarkoitetusta tehtäväkokonaisuudesta opettaja muotoili Kuvan 1 mukaisen tehtävän, jossa käsitellään alumiini- ja kuparikappaleiden jäähtymistä kalorimetrissä. Tehtävä koostui monivalintaväitteistä ja lämpöopin faktoista. Tehtävän ensimmäisessä vaiheessa opiskelijat ottivat kantaa monivalintaväitteisiin valitsemalla heidän mielestään lämpöopin sisältötiedon mukaiset väitteet. Tehtävän toisessa vaiheessa opiskelijat tarkastelivat valittuja väitteitä uudestaan ja valitsivat mitkä lämpöopin faktoista tukivat valittuja väitteitä. Lisäksi opiskelijat perustelivat miksi valittu fakta tuki tai ei tukenut tarkasteltavaa väitettä. Alla on esimerkki toivotusta päättelyketjusta, johon on alleviivattu oikea väite ja sitä tukevat faktat.
Kun kiehuvassa vedessä oleva alumiini- ja kuparikappale siirretään kalorimetrin kylmään veteen, kylmän veden lämpötila nousee. Tämä johtuu siitä, että kalorimetrin vesi ja kappaleet muodostavat termodynaamisen systeemin, joka hakeutuvat kohti tasapainoa siten, että lämpöenergia siirtyy kuumemmasta kappaleesta kylmempään, eli alumiini- ja kuparikappaleista veteen, jolloin veden lämpötila nousee. Lisäksi tulee huomioida, että kalorimetri on eristetty systeemi, joka ei vaihda energiaa ympäristön kanssa, minkä vuoksi alumiini- ja kuparikappaleiden lämpöenergia siirtyy ainoastaan kalorimetrin sisäpuolella olevaan veteen, eikä karkaa sen ulkopuolelle.
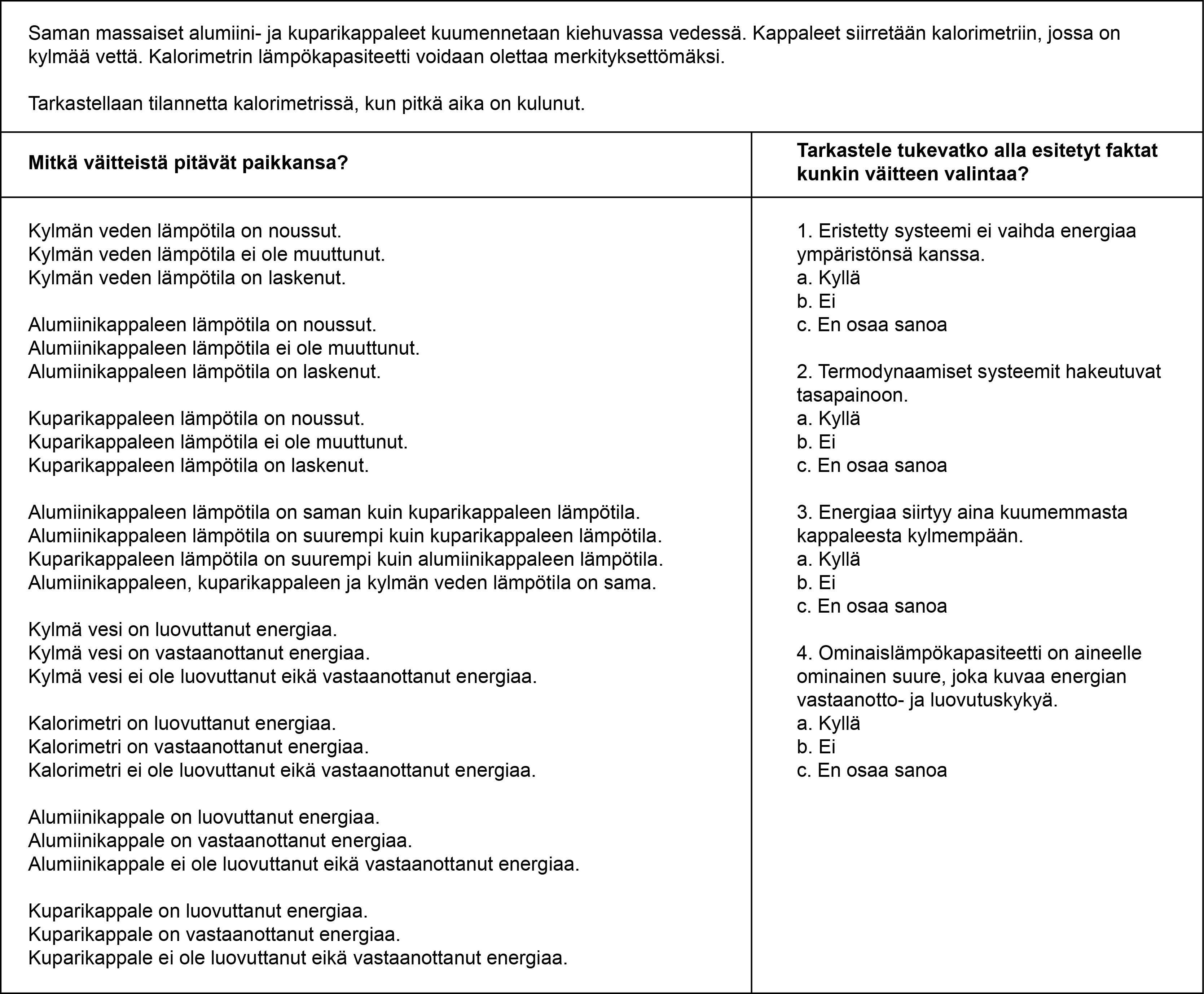
Harjoituskerran aikana väitteiden valinta toteutettiin sähköisellä kyselyllä, jonka opiskelijat täyttivät noin viidessä minuutissa. Tämän jälkeen valitut väitteet tarkastettiin. Seuraavaksi opettaja jakoi oppilaille sähköisen dokumentin, jossa arvioitiin kutakin oikeaksi tarkastettua väitettä Kuvan 1 faktojen avulla. Opiskelijat kopioivat dokumentin itselleen ja merkitsivät siihen
- kyllä, jos he olivat sitä mieltä, että tarkasteltava fakta tukee väitettä
- ei, jos he olivat sitä mieltä, että tarkasteltava fakta ei tue väitettä
- en osaa sanoa, jos he ovat sitä mieltä, että eivät voi sanoa tukeeko tarkasteltava fakta väitettä.
Opiskelijat kävivät läpi kaikki Kuvan 1 väitteet noin 10 minuutissa Tämän jälkeen opettaja kyseli mitkä faktoista 1-4 tukivat mitäkin Kuvan 1 väitettä ja kannusti opiskelijoita perustelemaan millä perusteella faktat voidaan nähdä väitteen perusteluna. Opettaja ei tässä vaiheessa antanut oikeita vastauksia vaan kannusti opiskelijoita aidosti pohtimaan mitä faktat tarkoittivat ja miten he voivat niiden avulla perustella oikeaksi tarkastettuja väitteitä. Valittujen faktojen läpikäyntiin käytettiin aikaa noin 35 minuuttia.
Laskennallinen tehtävä
Harjoituksen päätteeksi lukiolaiset aloittivat laskennallisen tehtävän, joka on esitetty Kuvassa 2. Tehtävän tarkoituksena oli havainnollistaa miten tehtävän lähtötiedoista ja lämpöopin faktoista voidaan muodostaa hyvin perusteltu ja loogisesti etenevä ratkaisu.

Tehtävän ratkaisua luonnosteltiin yhdessä siten, että opettaja kyseli opiskelijoilta mitä tehtävän tilanteesta tiedetään tai voidaan olettaa tiedettäväksi. Opettaja täydensi ratkaisun luonnosta opiskelijoilta tulleiden tietojen mukaan ja korosti, ettei tietojen tarvitse tässä vaiheessa olla vielä loogisessa järjestyksessä vaan ne voidaan jäsennellä lopuksi sähköisten työvälineiden avulla. Luonnosteluvaiheessa opiskelijat toivat esille
- tehtävän lähtötietoja, kuten alumiini- ja kuparikappaleen sekä veden alkulämpötilan: ${T_{Al}} = {T_{Cu}} = 100{\rm{\;^\circ C}} = 373,15\;{\rm{K}};\;{T_{vesi}} = 8\;{\rm{^\circ C}} = 281,15\;{\rm{K}}.$
- oletuksen, jonka mukaan kalorimetri muodostaa eristetyn systeemin, josta ei kulkeudu energiaa tai ainetta ympäristöön;
- lämpöopin faktoja, joiden mukaan lämpöenergia siirtyy kuumasta kappaleesta kylmempään, eli kupari- ja alumiinikappaleesta veteen, minkä seurauksena lämpötilaerot tasoittuvat ja kupari- ja alumiinikappale sekä vesi ovat lopuksi samassa lämpötilassa;
- tarpeen huomioida aineiden ominaislämpökapasiteetit tehtävän ratkaisussa.
Ominaislämpökapasiteetin huomioimiseksi opettaja muistutti, että lämpö on lämpötilaeron vuoksi siirtynyttä energiaa, jonka seurauksena lämpötilaerot tasaantuvat. Opettaja esitti lämmölle $Q$ kaavan $Q = cm\Delta T$, missä $c$ on kappaleen ominaislämpökapasiteetti, $m$ on kappaleen massa ja $\Delta T$ on tarkasteltavan kappaleen lämpötilan muutos. Tämän jälkeen opettaja ohjasi opiskelijoita muodostamaan suureyhtälön, jonka laatimiseksi opettaja esitti matemaattiset mallit alumiini- ja kuparikappaleen luovuttamalle ja veden vastaanottamalle lämpöenergialle:
${Q_{Al}} = {c_{Al}}{m_{Al}}\Delta {T_{Al}}$
${Q_{Cu}} = {c_{Cu}}{m_{Cu}}\Delta {T_{Cu}}$
${Q_{vesi}} = {c_{vesi}}{m_{vesi}}\Delta {T_{vesi}}$
Suureyhtälön viimeistelemiseksi opettaja painotti aikaisemmin tunnistettua faktaa, jonka mukaan kupari- ja alumiinikappaleiden lämpöenergia siirtyy veteen, mikä auttoi oppilaita muodostamaan yhtälön ${Q_{Al}} + {Q_{Cu}} = {Q_{vesi}}$. Tämän jälkeen suureyhtälö esitettiin muodossa
${c_{Al}}{m_{Al}}\Delta {T_{Al}} + {c_{Cu}}{m_{Cu}}\Delta {T_{Cu}} = {c_{vesi}}{m_{vesi}}\Delta {T_{vesi}}.$
Lopuksi opettaja muistutti, että kupari- ja alumiinikappaleen sekä veden loppulämpötila on sama: ${T_l} = {T_{l,Al}} = {T_{l,Cu}} = {T_{l,vesi}}$, mikä perusteella suureyhtälö voidaan esittää muodossa
${c_{Al}}{m_{Al}}\left( {{T_{Al}} – {T_l}} \right) + {c_{Cu}}{m_{Cu}}\left( {{T_{Cu}} – {T_l}} \right) = {c_{vesi}}{m_{vesi}}\left( {{T_l} – {T_{vesi}}} \right).$
Opiskelijoiden kotitehtäväksi jäi ratkaista suureyhtälöstä loppulämpötila ${T_l}$ joko kynän ja paperin avulla tai sähköisiä ohjelmia hyväksi käyttäen sekä laskea loppulämpötila.
Laskennallisen tehtävän ratkaisun laadintaan ja jäsentelyyn käytettiin aikaa noin 30 minuuttia.
Opettajan havainnot argumentointiharjoituksen käytöstä
Opettajan mukaan Kuvassa 1 esitetty tehtävä ohjaa opiskelijoita perustelemaan vastauksiaan FY2 Lämpö-kurssin keskeisillä opetussisällöillä, jotka on esitetty tehtävässä lämpöopin faktoina. Faktat auttavat opiskelijoita suuntaamaan ajatustyötään tehtävän kannalta relevantteihin fysiikan sisältöihin, mikä vähentää epärelevanttien, tehtävän ratkaisua usein vaikeuttavien fysiikan sisältöjen pohdintaa. Tehtävä siis ohjaa opiskelijan ajatustyötä niihin fysiikan sisältöihin, joita oppitunnilla on tarkoitus oppia. Lisäksi laskennallinen tehtävän tarkastelu tuo opiskelijoille näkyväksi hyvän fysiikan vastauksen piirteet ja sen millä tavoin fysiikan faktoja voidaan käyttää kaavojen käytön perusteluina.
Opettajan mukaan argumentointiharjoituksen vaikutus on ollut nähtävissä FY2 Lämpö -kurssikokeessa, jossa opiskelijat vastasivat vastaavanlaiseen kalorimetritehtävään. Aikaisempiin vuosiin verrattuna harjoituksen läpi käyneet opiskelijat perustelivat vastauksiaan poikkeuksellisen hyvin. Hyvin pärjäävien opiskelijoiden vastaukset ylittivät opettajan useiden vuosien opetuskokemuksen myötä muodostuneet ennakko-odotukset. Näissä vastauksissa kaavojen käyttöä perusteltiin kattavasti ja ristiriidattomasti lämpöopin käsitteisiin ja lainalaisuuksiin nojautuen. Heikommin pärjäävät opiskelijat olivat myös osanneet perustella vastauksiaan tavanomaista paremmin. Heidän vastauksissa oli nähtävissä tehtävien kannalta relevantteja, sanallisesti kuvattuja lämpöopin faktoja pelkkien kaavojen sijaan. Tämä kaavataudiksi kutsuttu ilmiö usein vaikeuttaa fysiikan oppimista [5], minkä vuoksi sanallisesti esitetyt kuvaukset voidaan nähdä oppimista tukevana edistysaskeleena.
Kokonaisuutena argumentointiharjoitus vaikuttaa lupaavalta tavalta tukea lukiolaisten perustelutaitojen kehittymistä. Tulevaisuudessa tämän tyyppisiä harjoituksia on tarkoitus kehittää etenkin FY1 Fysiikka luonnontieteenä -kurssille, jolloin jokainen lukiolainen saisi mahdollisuuden harjoitella luonnontieteille keskeisiä perustelutaitoja lukio-opintojen alkuvaiheessa. Näistä taidoista on varmasti hyötyä kaikille.
Yhteistyö kannattaa
Harjoituksen kehitystyön voidaan katsoa alkaneen MAOL:n syyspäivillä, joka toi yhteen opettajat ja monet matemaattisten aineiden koulutuksen parissa toimivat tahot, kuten LUMA SUOMI -verkostossa työskentelevät opetuksen tutkijat. Näiden osaajien yhteistyön seurauksena syntynyt argumentointiharjoitus on osoitus yhteistyön tärkeydestä ja siitä mitä ennakkoluuloton kokeilunhalu voi tuoda tullessaan.
Onnistuneen yhteistyön pohjalta suosittelemme tutkija-opettaja-yhteistyömallia, joka tähtää yhdessä laaditun opetuskokeilun toteuttamiseen ennalta sovittujen opetustavoitteiden pohjalta. Yhteistyön käynnistämiseksi opettajan ja tutkijan tulisi yhdessä tunnistaa opetustavoitteet, jotka he molemmat kokevat tärkeäksi, ja joiden saavuttamiseksi he ovat valmiita tekemään yhteistä suunnittelu-, valmistelu- ja arviointityötä. Tunnistettujen tavoitteiden saavuttamiseksi suunnitellaan opetuskokeilu ja laaditaan sen toteutusmateriaalit, joita hyödynnetään autenttisessa opetustilanteessa opetuskokeilun aikana. Kokeilun jälkeen sen toteutumista ja laadittuja materiaaleja arvioidaan opetustavoitteiden näkökulmista. Lopuksi kokeilun anti materiaaleineen jaetaan muiden opettajien, tutkijoiden ja asiasta kiinnostuneiden kesken.
Nämä yhteistyönvaiheet toteutuvat argumentointiharjoituksessa, joka on näyttäytynyt hyödyllisenä opettajalle, lukiolaisille ja luonnontieteiden opetuksen tutkijoille: Yhdessä olemme enemmän!
Lähteet ja viitteet
[1] OKM, Opetus- ja kulttuuriministeriö – Uusi lukio https://minedu.fi/uusilukio
[2] Opetushallitus, Lukion opetussuunnitelman perusteet 2015, 2015. https://www.oph.fi/saadokset_ja_ohjeet/opetussuunnitelmien_ja_tutkintojen_perusteet/lukiokoulutus. Haettu 29.4.2019.
[3] Lisätietoja argumentointia painottavasta luonnontieteiden kouluopetuksesta on osoitteissa:
[4] Katso tehtäväkokonaisuus Itä-Suomen yliopiston LUMA-keskuksen nettisivuilta: https://luma.uef.fi/3423/
[5] K. Kurki-Suonio ja R. Kurki-Suonio, Fysiikan merkitykset ja rakenteet, Helsinki: Limes ry, 1994.
Aloituskuva: Photo by Dominik Schröder on Unsplash







