Kvanttimekaniikan peruskysymyksiä: yhteismittauksista ja epätarkkuuksista
Kvanttimekaniikan synty ajoittuu 1920-luvun puoliväliin kun taas alkaneesta vuosikymmenestä odotetaan uutta kvanttivuosikymmentä kvanttiteknologioiden läpimurtoina. [1] Kvanttimekaniikka valmistui oleellisilta osiltaan hyvin nopeasti ja sen sovellusala on laajentunut moneen suuntaan atomaaristen ilmiöiden maailmasta. Kvanttimekaniikan abstrakti luonne synnytti kuitenkin kysymyksiä teorian tulkinnasta ja sen asemasta fysiikan keskeisenä perusteoriana. Odotukset alkaneesta uudesta kvanttivuosikymmenestä antavat ymmärtää, että joko nämä kysymykset on ratkaistu tai ne ovat epäolennaisia. Kvanttimekaniikan matemaattis-käsitteellinen perusta onkin merkittävällä tavalla selkiintynyt viime vuosikymmenten aikana ja vaikkei sen tulkintakiistoista olekaan kokonaan päästy irti niin teorialla on selkeä perustulkinta, eräänlainen minimitulkinta, josta ollaan oleellisesti yksimielisiä.
Tämän kirjoituksen tarkoitus on esitellä kvanttimekaniikan peruskysymyksiä uudemman tutkimuksen valossa pitäytyen oleellisesti tässä minimitulkinnassa. Kvanttimekaniikka epäkommutatiivisena todennäköisyysteoriana edellyttää matemaattisia tekniikoita, joita ei voi tässä yhteydessä esitellä. Teorian keskeiset piirteet saadaan kuitenkin esille jo tietyissä erikoistapauksissa, joissa matematiikan teknisen hallitsemisen vaatimus on vähäisempi ja voidaan tässä käyttää.
Kirjoituksen alkuun, Luku 1, on otettu asiaa vähemmän tunteville lyhyt katsaus kvanttimekaniikan ensimmäisestä kehitysvaiheesta vuosina 1925-1932. Luvussa 2 on esitelty yleistä probabilistista fysikaalista teoriaa klassisen mekaniikan ja kvanttimekaniikan yhdistävien ja erottavien piirteiden hahmottamiseksi. Luku 3 määrittelee tarkasteltavan erikoistapauksen, ns. kaksitasosysteemit tai kubittisysteemit, joiden tärkeitä reaalisaatoita ovat ns. spin-$\frac 12$-systeemit ja fotonit polarisaatio-ominaisuuksineen. Kvanttimekaniikan olennaisin (ja sen tulkintakiistoja aiheuttava) piirre, aito todennäköisyysluonne, esitellään luvussa 4. Kvanttimekaniikka epäkommutatiivisena todennäköisyysteoriana on synnyttänyt monenlaisia kysymyksiä mm. eri mittausten yhteensopivuudesta ja fysikaalisten suureiden yhteismitattavuudesta. Luvut 5 ja 6 esittelevät tähän liittyviä kysymyksiä. Luvuissa 7 ja 8 käsitellään mittauksen kvanttisysteemille aiheuttamaa häiriötä ja tarkastellaan kysymystä miten mittausvirhe ilmenee kvanttimekaniikassa. Loppulukua edeltävät luvut 9 ja 10 esittelevät Heisenbergin epätarkkuusrelaatioina tunnettuja preparointeja ja mittauksia koskevia rajoituksia.
1. Historiallista taustaa
Kun kaksikymmentäkolmevuotias Werner Heisenberg (1901-1976) julkaisi 95 vuotta sitten käänteentekevän artikkelinsa [2] fysiikan uuden perusteorian, kvanttimekaniikan matemaattisesta rakenteesta, otettiin luonnon kuvauksessa askel sellaiseen abstraktiuteen jota ei voitu ymmärtää klassisen fysiikan tavoin. Tästä seurannut ymmärrettävyyskriisi ilmeni seuraavina vuosikymmeninä kvanttimekaniikan tulkintakiistoina sekä dogmaattisina ja jopa vihamielisinä ”shut up and calculate” [3] asenteina nuoremman polven `epäileviä tuomaita’ kohtaan. Tilanne on oleellisesti muuttunut viimeisten vuosikymmenten aikana kvanttimekaniikan matemaattisen rakenteen ja sen perustulkinnan, minimitulkinnan, selkeytymisen myötä, mutta myös siksi, että koetekniikan kehittyminen ns. yksittäisobjektitasolle sekä ns. kvantti-informaation nousu ovat lisänneet yleistä mielenkiintoa teorian perusteisiin.
Kvanttimekaniikan alustava matemaattinen muotoilu hahmottui nopeasti Heisenbergin läpiämurtotyön jälkeen vuosina 1925-1926 Göttingenissä Heisenbergin, Max Bornin (1882-1970), ja Pascual Jordan (1902-1980) matriisimekaniikkana, ja Zürichissä Erwin Schrödingerin (1887-1961) aaltomekaniikkana. Myös Paul Diracin (1902-1984) töillä Cambridgessa oli tässä merkittävä osuus. Lisäksi teorian keskeiset tulkinnalliset elementit, Max Bornin todennäköisyystulkinta, Niels Bohrin (1885-1962) komplementaarisuusnäkökulma, sekä Heisenbergin epätarkkuusrelaatiot, olivat `selvillä’ jo vuonna 1927. Bohrin ja Heisenbergin ajatuksiin vaikutti oleellisella tavalla myös Wolfgang Pauli (1900-1958).
John von Neumannin (1903-1957) vuosina 1927-1931 julkaisemissa kuudessa matemaattisessa tutkimuksessa edellä mainitut kaksi kvanttimekaniikan sangen erilaisilta vaikuttavaa muotoilua, Heisenbergin ja Schrödingerin, osoittautuivat erikoistapauksiksi uudesta abstraktista teoriasta, niin sanotusta Hilbertin avaruus -kvanttimekaniikasta. Myös teorian todennäköisyysluonne sai selkeän matemaattisen ilmaisun von Neumannin tutkimuksissa, jotka hän tiivisti vuonna 1932 julkaistuun kirjaansa Mathematische Grundlagen der Quantenmechanik.
Heisenbergin 1925 ja Schrödingerin 1926 hahmottelemissa kvanttimekaniikan muotoiluissa uuden teorian outo ja abstrakti luonne tuli erityisen hyvin näkyviin siinä, että keskeiset klassisesta fysiikasta tutut perussuuret, dynaamiset muuttujat, kuten paikka ja liikemäärä, saivat matemaattiset esitykset, Heisenbergilla ääretönulotteisina matriiseina, Schrödingerillä differentiaalioperaattoreina, jotka eivät kommutoineet keskenään; jos paikka- ja liikemääräsuureita merkitään symboleilla $Q$ ja $P$, niin vastoin klassisen fysiikan odotusta, $QP=PQ$, näille suureille saatiin outo `vaihtorelaatio’ $QP=PQ+\imath\frac{h}{2\pi}$, missä $\imath=\sqrt{-1}$, $h$ on Planckin vakio, ja $\pi$ ympyrän kehän ja halkaisijan suhde.
Bohrin ja Heisenbergin esittämät ajatukset komplementaarisuudesta ja epätarkkuudesta olivat ensimmäisiä yrityksiä näiden matemaattisten relaatioiden fysikaalisen merkityksen ymmärtämiseksi. Hahmotellessaan (paperilla) erilaisia koejärjestelyjä paikka- ja liikemääräsuureiden yksikäsitteiseksi määrittelemiseksi ja mittaamiseksi Bohr tuli sellaiseen johtopäätökseen, että tällaiset koejärjestelyt ovat kaikki toisensa poissulkevia, niitä ei voida soveltaa yhdessä, matemaattisen relaation $QP-PQ=\imath\frac{h}{2\pi}$ ollessa tämä asiantilan muodollinen ilmaisu. Heisenberg yhtyi Bohrin näkemykseen, mutta hän otti rohkean lisäaskeleen: komplementaariset suureet voidaan määritellä ja mitata yhdessä, kunhan tarkkuuksista sopivasti tingitään. Välttämättömiksi määrittely- ja mittaustarkkuuksiksi Heisenberg esitti kuuluisat epätarkkuusrelaationsa: jotta paikka ja liikemäärä voidaan mitata yhdessä, niiden mittaustarkkuuksien $\delta q$ ja $\delta p$ on toteutettava ehto $\delta q\cdot\delta p\sim h$. Intuitiivisten ja semiklassisten tarkastelujensa lisäksi Heisenberg ei kuitenkaan sen paremmin määritellyt $\delta$-suureitaan kuin johtanut niille mitään matemaattista relaatiota alulle panemansa uuden teorian puitteissa.
Bohrin ja Heisenbergin töiden johdosta von Neumann sisällytti kirjaansa laajat jaksot fysikaalisten suureiden samanaikaisesta mitattavuudesta sekä itse mittaustapahtuman kvanttimekaanisesta kuvauksesta. Tämän problematiikan käsitteellisesti huolellinen ja matemaattisesti tarkka analyysi johti yhteen monista von Neumannin lauseina tunnetuista tuloksista: annetut fysikaaliset suureet voidaan mitata yhdessä tarkalleen silloin, kun näitä suureita vastaavat operaattorit, Heisenbergin mielessä matriisit, Schrödingerin mielessä differentiaalioperaattorit, kommutoivat keskenään. Koska $QP\ne PQ$, niin paikkaa ja liikemäärää ei siis voi mitata yhdessä. Heisenbergin epätarkkuusrelaatioilleen antama mittaustarkkuustulkinta jäi kuitenkin vuosikymmenten ajaksi arvoitukseksi.
Von Neumannin monumentaalinen työ tiivisti kvanttimekaniikan ensimmäisen vaiheen perustetutkimukset yhtenäiseksi abstraktiksi teoriaksi, kompleksisen separoituvan ääretönulotteisen Hilbertin avaruuden operaattoriteoriaksi. Nykynäkökulmasta teoriassa oli kuitenkin fysikaalisen suureen matemaattiseen esitykseen liittyvä rajoitus, joka pitkitti teorian käsitteellisen perustan selkeytymistä. Tässä kirjoituksessa pyritään valaisemaan tätä teoriaa, erityisesti sen epäkommutatiivisuudesta aiheutuvaa fysikaalisten suureiden yhteismittausongelmaa, ja antaa samalla vaikutelman kvanttimekaniikan vaatiman uuden ajattelun ja siihen liittyvän matematiikan luonteesta sellaisessa erikoistapauksesssa, jossa matematiikan teknisen hallitsemisen vaatimus on minimoitu, mutta uuden ajattelutavan luonne kuitenkin tulee esiin.
Kvanttimekaniikan, niin kuin yleensäkin matemaattisesti muotoiltujen fysiikan teorioiden, yhteydessä on tapana käyttää kieltä, jossa varsinaisesti matemaattisista objekteista puhutaan niiden fysikaalisten tulkintojen mukaisella terminologialla. Tämä tapa voi aiheuttaa sekaannusta, jota voidaan minimoida, jos lukija (kirjoittajan toivottavasti avustamana) tiedostaa selvästi, millainen tulkinta puhetavan taustalla on.
2. Fysiikka ja todennäköisyys: klassisen mekaniikan ja kvanttimekaniikan yhdistäviä ja erottavia piirteitä
Tilastollinen kausaliteetti. Kvanttimekaniikan(kin) perusrakenne saadaan esille tarkastelemalla fysikaalisen kokeen yleistä periaatteellista asetelmaa yksinkertaisena kolmivaiheisena preparointi — mittaus — tuloksen rekisteröinti -prosessina: fysikaalinen systeemi preparoidaan mittausta varten halutulla tavalla, määritellään sopivat alkuehdot, suoritetaan haluttu mittaus ja tulos rekisteröidään. Jotta tällaisella kokeella olisi merkitystä, rekisteröidyn mittaustuloksen tulisi riippua, paitsi suoritetusta mittauksesta, myös siitä, miten systeemi on preparoitu. Käytännössä systeemin (saman tai ”identtisen”) ”samalla” tavalla suoritettu preparointi ei kuitenkaan välttämättä johda samaan mittaustulokseen, vaan mittaustuloksia kuvaa jokin empiirinen jakauma. Näin on jo klassisen fysiikan tapauksessa, josta arkinen nopan heitto on kaikille tuttu esimerkki. Matemaattiseen malliin tulee näin mukaan todennäköisyyksiä. Todennäköisyysteoria sinänsä on matematiikan haara. Kun halutaan soveltaa sitä matematiikan ulkopuolelle, tavallinen tapa (joka tässä kirjoituksessa on tausta-ajatuksena) on käyttää toistokokeisiin liittyvää suhteellisen frekvenssin raja-arvo -tulkintaa, jonka eräänlaisena perusteluna ovat suurten lukujen lain erilaiset variantit.
Tässä kirjoituksessa käytetään toisinaan ilmaisua tilastollinen kausaliteetti, jolla on seuraava sisältö:
- kun sama prosessi toistetaan monta kertaa, joko samalla tai identtisillä systeemeillä, niin mittaustulosten suhteelliset esiintymistaajuudet approksimoivat preparoinnista ja mittauksesta riippuvia todennäköisyyksiä.
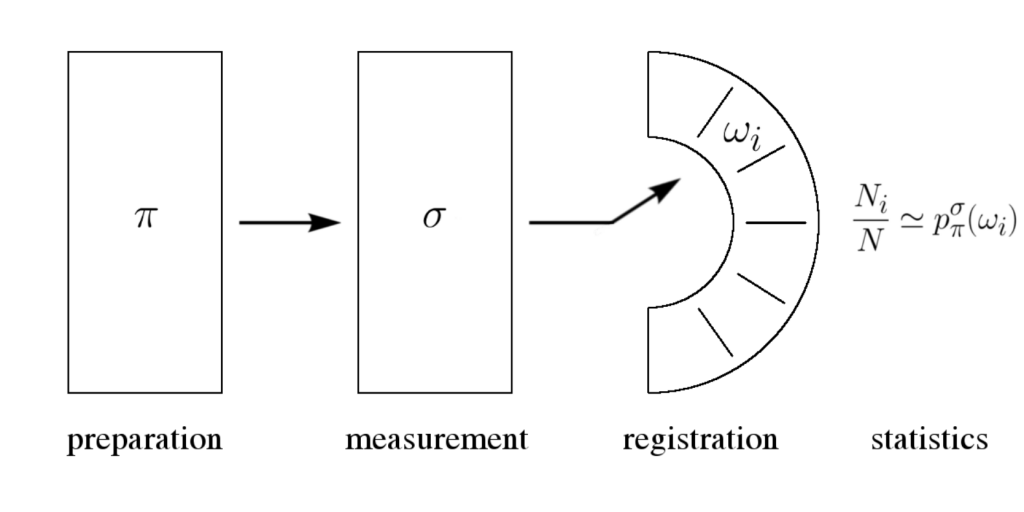
Tässä mainitut todennäköisyydet ovat preparointia ja mittausta kuvaavaan malliin liittyviä (matemaattisia) käsitteitä todennäköisyysteorian mielessä, ja mittaustulosten suhteelliset esiintymistaajuudet puolestaan tulevat esiin kokeissa, joissa tätä mallia testataan. Tilastollisen kausaliteetin ajatus samoin kuin siihen liittyvä approksimointi on luonnollisesti idealisaatio, jonka tarkoitus on periaatteessa liittää matemaattinen malli kokeisiin. Tämä yleinen ehto on sekä klassisen mekaniikan että kvanttimekaniikan taustalla. Näiden kahden teorian ominaispiirteiden erittelemiseksi tarkastellaan vielä tilastolliselle kausaliteetille perustuvaa yleistä teoriaa menemättä kuitenkaan teknisiin yksityiskohtiin. [4]
Tilastolliselle kausaliteetille rakentuvassa todennäköisyysteoreettisessa lähestymistavassa tilastollisesti erottautumattomat preparoinnit on tyypillistä samastaa fysikaalisen systeemin tilan käsitteeksi, kun taas tilastollisesti erottautumattomat mittaukset samastetaan fysikaalisen suureeen käsitteeksi. Tämä sisältää erityisesti sen ilmeisen tosiasian, että mikä tahansa suure voidaan mitata usealla eri tavalla, joka tulee esille myös teorian yksityiskohtaisemmassa kehittelyssä.
Mittauksen ja siis fysikaalisen suureen spesifioiminen edellyttää, paitsi sen keskeisten symmetriaominaisuuksien määrittelemistä, myös sen arvojoukon $\Omega$ ja sopivan osajoukkokokoelman $\mathcal{A}\subset\{X\,|\, X\subset\Omega\}$ valintaa. Intuitiivisesti (abstrakti matemaattinen) joukko $\Omega$ on suureen mahdollisten mittaustulosten joukko, kun taas joukot $X\in\mathcal{A}$ ovat ns. testijoukkoja, joihin mittaustulokset $\omega\in\Omega$ rekisteröityvät. Todennäköisyysteoriassa yleisesti käytössä olevaan tapaan osajoukkokokoelmalta $\mathcal{A}$ vaaditaan $\sigma$-algebran rakenne. [5]
Tyypillisesti joukko $\Omega$ on joko koko reaalisuora $\mathbb{R}$ tai sen sopiva osajoukko. Oletamme, että näin on, vaikka käytämme yleistä merkintää $(\Omega,\mathcal{A})$ suureen $O$ arvojoukolle ja valituille testijoukoille. Yksinkertaisimmassa tapauksessa joukko $\Omega$ on kahden alkion joukko, esimerkiksi $\{-1,1\}$, jolloin $\mathcal{A}$ koostuu tyhjästä joukosta $\emptyset$, koko joukosta $\{-1,1\}$ ja yksiöistä $\{-1\}$ ja $\{1\}$. Tällaiset kaksiarvoiset suureet vastaavat ns. kyllä-ei -kokeita: tulos rekisteröidään joukossa $X\subset\Omega$ tai sen ulkopuolella $\Omega\setminus X$.
Olkoot $\boldsymbol{S}$ ja $\boldsymbol{O}$ annetun fysikaalisen systeemin kaikkien tilojen sekä suureiden (abstraktit) joukot. Tilastollisen kausaliteetin vaatimuksen mukaisesti oletamme, että
- jokainen tila $s\in \boldsymbol{S}$ ja suure $O\in \boldsymbol{O}$, arvojoukolla $(\Omega,\mathcal{A})$, määrittelee todennäköisyysmitan $p^O_s:\mathcal{A}\to[0,1]$,
Huomautus 1. On paikallaan korostaa, että todennäköisyysmitta $p^O_s$ on $\sigma$-algebrassa $\mathcal{A}$ määritelty joukkofunktio, joka saa arvoja reaalilukuväliltä $[0,1]$, on numeroituvasti additiivinen yli erillisten joukkojen, ts., $p^O_s(\cup_i X_i)=\sum_i p^O_s(X_i)$, aina kun joukot $X_i\in\mathcal{A}$ ovat erillisiä ($ X_i\cap X_j=\emptyset, i\ne j$), ja lisäksi $p^O_s(\Omega)=1$. Kolmikko $(\Omega,\mathcal{A}, p^O_s)$ on esimerkki Andrei Kolmogorovin (1903–1987) vuonna 1933 aksiomaattisesti muotoilemasta todennäköisyysavaruudesta. Kaksiarvoisen suureen $O$ tapauksessa mitta $p^O_s$ saa (lukujen 0 ja 1 lisäksi) vain arvot $p^O_s(\{1\})$ ja $p^O_s(\{0\})=1-p^O_s(\{1\})$.
Huomattakoon, että näin muotoiltuun teoriaan on sisäänrakennettuna tilastollinen täydellisyys: jos $p^O_{s_1}=p^O_{s_2}$ kaikilla suureilla $O$, niin $s_1=s_2$, ja jos $p^{O_1}_s=p^{O_2}_s$ kaikilla tiloilla $s$, niin $O_1=O_2$. [6]
Asettamalla joukoille $\boldsymbol{S}$ ja $\boldsymbol{O}$ fysikaalisesti motivoituja lisäehtoja ja pitäytymällä tilastollisen kausaliteetin vaatimuksessa voidaan näin hahmotellun teorian rakennetta tarkentaa. Tarkastellaan vielä lyhyesti eräitä tällaisia ehtoja.
Tilajoukko on konveksi. Kuvitellaan aluksi, että suoritamme jonkin suureen $O$ (toisto)mittauksen niin, että osa toistoista, suhteellisella osuudella $0\leq\lambda\leq 1$, suoritetaan systeemin ollessa tilassa $s_1$, ja osa, suhteellisella osuudella $1-\lambda$, tilassa $s_2$. Tällöin kokonaismittaustulostilastoksi saadaan kyseisten tilastojen painotettu summa, jota todennäköisyysmitta $\lambda p^O_{s_1}+(1-\lambda)p^O_{s_2}$ kuvaa. Nyt voidaan kysyä, onko jokaista $s_1,s_2,0\leq\lambda\leq 1$ kohti olemassa sellainen tila $s=s(s_1,s_2,\lambda)$, jolle $p^O_s=\lambda p^O_{s_1}+(1-\lambda)p^O_{s_2}$ kaikilla suureilla $O$; jos on, niin teorian perusrakenteen nojalla niitä on vain yksi. Olettamus tällaisen tilan olemassaolosta on harmiton siinä mielessä, että jos tilajoukko ei alunperin sisällä tällaista tilaa, se voidaan yksinkertaisesti lisätä siihen. Se antaa kuitenkin tilajoukolle $\boldsymbol{S}$ tärkeän perusrakenteen, ns. konveksin (kuperan) joukon rakenteen, joka puolestaan avaa uusia mahdollisuuksia tilajoukon $\boldsymbol{S}$ mahdollisten lisärakenteiden tutkimiseksi.
Ensinnäkin voidaan kysyä, onko joukossa $\boldsymbol{S}$ sellaisia tiloja $s$, joita ei voida lausua epätriviaalilla tavalla muodossa $s=\lambda s_1+(1-\lambda)s_2$. [7] Tällaiset tilat, jos niitä on, ovat tilajoukon $\boldsymbol{S}$ ääripisteitä, ns. puhtaita tiloja. Sekä klassisen mekaniikan että kvanttimekaniikan tilajoukot ovat konvekseja, ja tällaisia puhtaita tiloja on jopa niin runsaasti, että mikä tahansa muu tila, ns. sekoitettu tila, voidaan lausua puhtaiden tilojen (mahdollisesti matemaattisen mittateorian mielessä yleistettynä) konveksikombinaationa.
Klassista ja kvanttimekaniikkaa erottavana piirteenä saadaan tällöin esille kysymys sekoitetun tilan mahdollisesta yksikäsitteisestä esittämisestä puhtaiden tilojen avulla. Klassisessa mekaniikassa tämä yksikäsitteisyys on voimassa, kvanttimekaniikassa ei koskaan (siis ei millekään sekoitetulle tilalle). Tällä seikalla on tärkeä merkitys mittaustulostodennäköisyyksien mahdolliselle syvällisemmälle tulkinnalle: klassisessa mekaniikassa todennäköisyysennusteisiin päätyminen voidaan periaatteessa tulkita tietämättömyydeksi systeemin tosiasiallisesta tilasta (alkuehdoista), kvanttimekaniikassa tällaista tulkintaa ei voi perustella.
Esimerkki 1. Tason kolmio ja ympyrälevy ovat esimerkkejä konvekseista joukoista; kolmion tapauksessa sen kärjet ovat ääripisteet, ja sen muut pisteet voidaan esittää vain yhdellä tavalla kärkipisteiden konveksikombinaationa. Ympyrälevyn ääripisteet ovat sen kehän pisteet, ja mikä tahansa ympyrän sisäpiste voidaan lausua mielivaltaisen monella tavalla kehän pisteiden konveksikombinaationa. Konveksi joukko sisältää aina myös pisteidensä yhdysjanat.

Puhtaiden tilojen superpositiot. Toinen klassista mekaniikkaa ja kvanttimekaniikkaa erottava tiloja koskeva erityispiirre saadaan myös helposti esille mittaustulostodennäköisyyksien avulla. Olkoon tila $s$ tilojen $s_1$ ja $s_2$ seos painolla $\lambda$, $s=\lambda s_1+(1-\lambda)s_2, 0\ne\lambda\ne 1 $. Tila $s$ on seuraavassa probabilistisessa mielessä tilojen $s_1$ ja $s_2$ välissä (Diracin terminologia): jokaisella suureella $O$ ja testijoukolla $X$, jos $p^O_{s_1}(X)=p^O_{s_2}(X)=0$, niin myös $p^O_s(X)=0$. Voidaan kysyä onko mahdollista, että jokin puhdas tila olisi tässä mielessä joidenkin muiden puhtaiden tilojen välissä. Klassinen mekaniikka ei sisällä tällaista mahdollisuutta. Sen sijaan kvanttimekaniikan mukaan jokainen puhdas tila on jopa mielivaltaisen monella eri tavalla joidenkin muiden puhtaiden tilojen välissä. Jos puhdas tila $s$ on puhtaiden tilojen $s_1$ ja $s_2$ välissä yllä mainitussa mielessä, niin sanomme että tila $s$ on tilojen $s_1$ ja $s_2$ superpositio.
Taustatietoa 1. Yksittäisobjekteilla suoritetut kvanttifysikaaliset kaksoisrakokokeet ovat puhtaiden tilojen superponoitumisen yksi suorimmista ja vaikuttavimmista kokeellisista todennuksista. Tällaisia kokeita on suoritettu mm. fotoneilla, neutroneilla, elektroneilla, atomeilla ja molekyyleillä. [8] Ehkä hämmästyttävin näistä on Akira Tonomuran (1942-2012) 1987 toteuttama koe elektroneilla. Koe oli klassisen Youngin kokeen puhdasoppinen toteutus yksittäisillä elektroneilla. Kuva 3 esittää kokeen kaaviomaisesti. Tässä Youngin viivaimena käytettiin hyvin ohutta positiivisen sähkövarauksen omaavaa nauhaa, jonka paksuus oli noin millin tuhannesosa, siis noin 1 $\mu m$. Nauha oli asetettu kahden 1 cm etäisyydellä toisistaan olevan maadoitetun levyn väliin. Elektronit kiihdytettiin 150 000 km/s vauhtiin, jolloin niiden de Broglien aallonpituus oli 0,005 nm. [9] Elektronivirta lähteestä oli 1000 elektronia sekunnissa, joten elektronien keskimääräinen laskennallinen etäisyys oli 150 km.

Laitteen pituus oli 150 cm. Elektroni havaittiin paikkaherkällä havaintolevyllä (jossa käytettiin 2000-kertaista suurennosta havaintopisteiden erottamiseksi toisistaan). Elektronien iskeytymistä havaintolevylle pystyttiin seuraamaan elektroni elektronilta: Ensimmäiset elektronit näyttivät iskeytyvän levylle täysin satunnaisesti, ja vaikutelma säilyi samana noin 1000 ensimmäisen elektronin osalta. Kun elektroneja oli kertynyt havaintolevylle jo useita tuhansia, iskeytymiskohdista alkoi hahmottua tilastollinen interferenssikuvio, joka kirkastui täysin selväksi 20 minuutin kokonaismittausaikana, jolloin varjostimelle oli saatu noin 70 000 elektronia (ks. kuvasarja $a-d$). Koetuloksen muotoutumista seurattiin myös televisioruudulla ja se on yhä kaikkien nähtävissä. [11]
Oletetaan, että puhtaat tilat $s_1$ ja $s_2$ edustavat elektronin kahta (klassisesti) mahdollista reittiä lähteestä varjostimelle nauhan vasemmalta ja oikealta puolelta. Jos elektronin tila havaintolevylle iskeytyessään olisi näiden tilojen seos, esim. painoilla $\frac 12$, niin elektronien kokonaiskertymässä havaintolevylle pitäisi erottua kaksi erillistä läiskää vastaten näitä eri reittejä. Koetulos ei tue tätä olettamusta mutta on sopusoinnussa sen kanssa että elektroni havaintolevylle iskeytyessään olisi puhtaassa tilassa joka on kyseisten puhtaiden tilojen (tasavahva) superpositio.
Suureiden yhteismitattavuus. Tarkastellaan vielä lyhyesti mahdollisuutta yhdistää kahden tai useamman suureen mittauksia niiden yhteismittauksiksi. Koska kukin fysikaalinen suure $O$ määräytyy täysin todennäköisyysmittojensa $p^O_s, s\in$ $\boldsymbol{S}$, kuvaamista mittaustulostilastoista, niin kysymys kahden (tai useamman) suureen $O_1$ ja $O_2$ yhdistetystä mittauksesta palautuu kysymykseen, onko olemassa suure $O$, jonka mittaustulosjakaumista $p^O_s$ suureiden $O_1$ ja $O_2$ mittaustulosjakaumat $p^{O_1}_s$ ja $p^{O_2}_s$ voidaan rekonstruoida sopivalla tavalla. Yksi luonnollinen muotoilu tälle on seuraava: [12] on olemassa sellaiset funktiot $f_1$ ja $f_2$, jotka yhdistävät suureen $O$ arvojoukon $\Omega$ suureiden $O_1$ ja $O_2$ arvojoukkoihin $\Omega_1$ ja $\Omega_2$, $f_1:\Omega\to\Omega_1$ ja $f_2:\Omega\to\Omega_2$, yhdistäen samalla niiden testijoukot keskenään (alkukuvakuvauksin), $\mathcal{A}_1\ni X\mapsto f_1^{-1}(X)\in\mathcal{A}$ ja $\mathcal{A}_2\ni Y\mapsto f_2^{-1}(Y)\in\mathcal{A}$, niin, että
| (2.1) | $ p^{O_1}_s(X)=p^{O}_s(f_1^{-1}(X))\qquad\quad p^{O_2}_s(Y)=p^{O}_s(f_2^{-1}(Y)).$ |
Jos tämä ehto toteutuu kaikilla testijoukoilla $X$ ja $Y$ sekä kaikilla tiloilla $s$, niin suureet $O_1$ ja $O_2$ määräytyvät täysin suureen $O$ mittaustulostilastoista ja sanomme, että ne voidaan mitata yhdessä.
Esimerkki 2. Ehto 2.1 yhdistää suureiden $O_1$ ja $O_2$ mittaustulostilastot suureen $O$ mittaustulostilastoihin. Tästä yksinkertaisena esimerkkinä olkoot $(p,1-p)$ ja $(q,1-q)$ kahden kaksiarvoisen suureen $O_1$ ja $O_2$ (arvojoukkoina $\{\omega_1,\omega_1’\}$ ja $\{\omega_2,\omega_2’\}$) sekä $(r,s,t,u)$ neliarvoisen suureen $O$ (arvojoukkona $\{a,b,c,d\}$) mittaustulostodennäköisyydet tilassa $s$. Jos $p=r+t$, ja siis $1-p=s+u$, ja $q=r+s$, ja siis $1-q=t+u$, niin $O$-mittaus tilassa $s$ reaalisoi myös suureiden $O_1$ ja $O_2$ mittauksen tilassa $s$, funktioin $f_i:\{a,b,c,d\}\to\{\omega_i,\omega_i’\}, i=1,2$, kun $f_1(a)=f_1(c)=\omega_1, f_1(b)=f_1(d)=\omega_1’$ ja $f_2(a)=f_2(b)=\omega_2,f_2(c)=f_2(d)=\omega_2’$. Jos tämä toteutuu kaikilla tiloilla $s$ niin $O$ on $O_1$:n ja $O_2$:n (eräs) yhteismittaus.
Parille ($\boldsymbol{S}$, $\boldsymbol{O}$) rakentuvan teorian hahmottelemiseksi tässä avautuvat muun muassa seuraavat kaksi mahdollisuutta: jokainen suurepari $(O_1,O_2)$ voidaan mitata yhdessä; jokaista suuretta $O_1$ kohti on olemassa suure $O_2$, jota ei voida mitata yhdessä suureen $O_1$ kanssa. Klassinen mekaniikka on esimerkki ensimmäisestä mahdollisuudesta, kvanttimekaniikassa toteutuu jälkimmäinen vaihtoehto. Bohrin tarkastelut tiettyjen suureiden mittaamiseen soveltuvien koejärjestelyjen toisensa poissulkevuudesta ovat sopusoinnussa tämän kvanttimekaniikan tuloksen kanssa.
Mahdollisuus mitata kaksi (tai useampi) suuretta yhdessä on läheisessä yhteydessä kysymykseen, voidaanko nämä suureet mitata toinen toisensa jälkeen niin, että mittausjärjestyksellä ei ole lopputuloksen kannalta merkitystä. Jonomittaus asettaa ensin suoritetulle mittaukselle ilmeisen lisävaatimuksen: ensimmäisen mittauksen jälkeen systeemille pitää vielä voida suorittaa toinen mittaus. Vaikka tämä ehto toteutuisikin, eli systeemi ei `tuhoudu’ ensimmäisessä mittauksessa, niin kyseinen mittaus voi silti muuntaa systeemiä. Tämän kysymyksen tarkempi analyysi edellyttää systeemin mittauksessa kokeman muutoksen kuvaamista. Palaamme asiaan luvussa 7. Todettakoon kuitenkin, että jos tällaisen jonomittauksen tulos on järjestysriippumaton niin suureet voidaan mitata myös yhdessä. On selvää, että jopa klassisessa fysiikassa jonomittaukset eivät välttämättä ole järjestysriippumattomia.
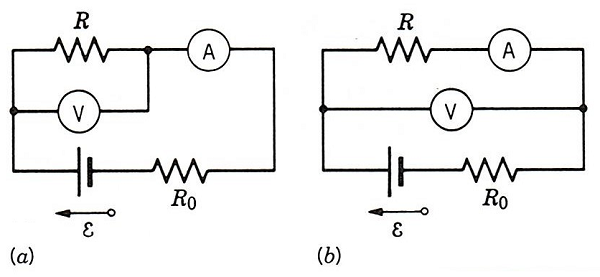
Esimerkki 3. Yksinkertainen mutta kuvaava esimerkki järjestysriippuvasta mittausparista saadaan jännitelähde-laite -virtapiiristä, josta halutaan mitata laitteen läpi kulkeva virta sekä siinä tapahtuva jännitehäviö, esimerkiksi tehon määrittämiseksi. Laitteen $\boldsymbol{L}(R)$ läpi kulkeva virta $I$ voidaan mitata virtamittarilla $\boldsymbol{A}$ sekä laitteessa tapahtuva jännitehäviö $U$ jännitemittarilla $\boldsymbol{V}$. Kumpikin mittaus voidaan luonnollisesti suorittaa toisistaan riippumattomasti erikseen samalla virtapiirillä. Tällöin jää kuitenkin epäily siitä liittyvätkö saadut $I$ ja $U$ arvot tarkalleen samaan virtapiiriin, onko jännitelähde ja/tai laite mahdollisesti muuttunut kytkentöjä vaihdettaessa. Tämän epäilyn välttämiseksi voimme kytkeä molemmat mittalaitteet samaan virtapiiriin mutta tällöin on valittava kahden toisensa poissulkevan vaihtoehdon välillä: joko saadaan oikea virran arvo $I$ jolloin jännitehäviöksi saadaan laitteen ja virtamittarin yhteinen jännitehäviö $U’$, tai saadaan oikea jännitehäviö $U$, mutta tällöin virtamittarin lukemana saadaan sekä laitteen $\boldsymbol{L}$ että jännitemittarin $\boldsymbol{V}$ läpi kulkeva kokonaisvirta $I’$. Kummassakin tapauksessa `virhe’, $U’-U$, tai $I’-I$, voidaan kuitenkin paitsi kompensoida niin myös `valita’ mielivaltaisen pieneksi sopivalla mittalaitteen $\boldsymbol{V}/\boldsymbol{A}$ valinnalla. Jos virtamittarin sisäinen vastus $R_{\boldsymbol{A}}$ tunnetaan, niin ensimmäisessä tapauksessa saadaan $U’-U=R_{\boldsymbol{A}}I$ ($\to 0$ kun $R_{\boldsymbol{A}}\to 0$), ja jos $R_{\boldsymbol{V}}$ on jännitemittarin sisäinen vastus, niin saadaan $I’-I=U/R_{\boldsymbol{V}}$ ($\to 0$, kun $R_{\boldsymbol{V}}\to \infty$). Kvanttimekaniikassa sen paremmin virheen kompensointi kuin sen eliminointikaan ei tyypillisesti ole mahdollista.
*****
Emme kehittele yleistä teoriaa tämän pidemmälle. Todettakoon kuitenkin, että tässä hahmotellun lähestymistavan puitteissa voidaan luetella joukko pääasiassa fysikaalisesti motivoituja olettamuksia, teorian aksioomat, jotka määräävät tilajoukon $\boldsymbol{S}$ ja suurejoukon $\boldsymbol{O}$ sekä todennäköisyysmittojen $p^O_s:\mathcal{A}\to[0,1]$ rakenteet kompleksisen separoituvan ääretönulotteisen Hilbertin avaruuden matemaattisina objekteina. Takana on luonnollisesti aimo annos epätriviaalia matematiikkaa. Se osoittaa kuitenkin, missä mielessä kyseinen teoria on välttämätön. Kvanttimekaniikan minimitulkinnalla tarkoitetaan juuri pitäytymistä tila-suure pareihin $(s,O)$ liittyvien todennäköisyyksien $p^O_s(X), X\in\mathcal{A},$ mittaustulostilasto -tulkintaan.
3. Spin-$\frac 12$-objektit — kubitit
Kvanttimekaniikan mukaan sellaisilla fysikaalisilla systeemeillä kuin esimerkiksi elektroni, neutroni tai fotoni on ilmeisten avaruudellisten ominaisuuksiensa (kuten paikka ja liikemäärä) lisäksi ns. sisäisiä ominaisuuksia (vapausasteita, kuten spin ja polarisaatio), joita voidaan kuvata äärellisulotteisessa Hilbertin avaruudessa, sen operaattoriteoriana. [13] Näistä yksinkertaisin (epätriviaali) on kaksiulotteinen avaruus jonka avulla saadaan jo kuvattua yllä mainitut elektronin ja neutronin spinominaisuudet sekä fotonin polarisaatio-ominaisuudet. [14] Tämän matemaattisesti yksinkertaisen mallin avulla saadaan kuitenkin esille lähes kaikki kvanttimekaniikan erityispiirteet, [15] joten tyydymme tässä kirjoituksessa eräitä hajahuomioita lukuun ottamatta tähän malliin. Kvanttimekaniikan informaatioteoreettisissa sovelluksissa tällaisia kaksitasosysteemejä on tapana kutsua kubittisysteemeiksi, tai vain kubiteiksi, kun käytettävää systeemiä, ”informaation kantajaa”, ei ole tarve erikseen spesifioida.
Esittelemme seuraavassa lyhyesti tätä mallia ja käytämme spin-$\frac 12$-objekteihin liittyvää terminologiaa, eli puhumme spintiloista ja spinsuureista (muistaen kuitenkin, että kysymys on matemaattisista objekteista). Vaihtoehtoisena puhetapana olisi polarisaatiotilat ja polarisaatiosuureet tai kubittitilat ja kubittisuureet.
Äärellisulotteisen kompleksisen Hilbertin avaruuden perusrakenne ja sen operaattoriteoriaa on esitelty lyhyesti kirjoituksen liitteessä. Kuten siellä on esitetty, kaksiulotteinen kompleksinen Hilbertin avaruus voidaan samaistaa kompleksilukuparien $(z,w), z,w\in\mathbb{C}$, muodostamalle vektoriavaruudelle $\mathbb{C}^2$, jossa vektorien $(z,w)$ ja $(u,v)$ sisätulo on $\left\langle{(z,w)}|{(u,v)}\right\rangle=\bar zu+\bar wv$ ja siitä saatava vektorin $(z,w)$ pituus on $\left\|{(z,w)}\right\|=\sqrt{|z|^2+|w|^2}$, missä $\bar z$ on kompleksiluvun $z$ kompleksikonjugaatti ja $|z|=\sqrt{\bar zz}$ sen itseisasrvo. Hilbertin avaruuden $\mathbb{C}^2$ operaattorit, lineaarikuvaukset, voidaan antaa $2\times 2$ -kompleksimatriiseina ja niiden ominaisuudet saadaan matriisien ominaisuuksina. Olkoon $M(\mathbb{C}^2)$ kaikkien tällaisten matriisien joukko. Spin-$\frac 12$-objektien, kubittien, kvanttiteoria rakentuu siis vektoriavaruudelle $\mathbb{C}^2$ ja sen operaattoriavaruudelle $M(\mathbb{C}^2)$ luvussa 2 esiteltyjen yleisten periaatteiden mukaisesti.
Taustatietoa 2. Vektoriavaruuden $\mathbb{C}^2$ lineaarikuvaukset voidaan antaa matriiseina $(a_{ij}), a_{ij}\in\mathbb{C}, i,j=1,2$. Kuten vektorit niin myös matriisit voidaan lausua yksikäsitteisellä tavalla valitun kannan avulla. Erään $M(\mathbb{C}^2)$:n tärkeän kantamatriisijoukon muodostavat ns. Paulin matriisit
| $ I= \left(\begin{matrix} 1& 0 \\ 0&1\end{matrix}\right), \ \sigma_1= \left(\begin{matrix} 0& 1 \\ 1&0\end{matrix}\right), \ \sigma_2=\left(\begin{matrix} 0& -\imath \\ \imath&0\end{matrix}\right), \ \sigma_3=\left(\begin{matrix} 1& 0 \\ 0&-1\end{matrix}\right),$ |
joiden avulla matriisi $(a_{ij})$ voidaan lausua muodossa $ A= a_0 I+a_1\sigma_1+a_2\sigma_2+a_3\sigma_3$, missä käytetyt kertoimet $a_0,a_1,a_2,a_3$ saadaan matriisialkioiden $a_{ij}$ avulla seuraavasti: $a_0=\frac 12(a_{11}+a_{22})$, $a_1=\frac 12(a_{12}+a_{21})$, $a_2= \frac i2(a_{12}-a_{21})$, $a_3= \frac 12(a_{11}-a_{22})$.
Kvanttimekaniikalle tärkeitä matriiseja ovat itseadjungoidut eli Hermiten matriisit, siis matriisit, joiden transpoosin kompleksikonjugaatti on matriisi itse,
| $ A=\left(\begin{matrix} a_{11}&a_{12}\\ a_{21}&a_{22} \end{matrix}\right)= \left(\begin{matrix} \overline{a_{11}}&\overline{a_{21}}\\ \overline{a_{12}}&\overline{a_{22}} \end{matrix}\right) = A^*.$ |
Huomaamme, että näin on tarkalleen silloin, kun esityksessä $ A= a_0 I+a_1\sigma_1+a_2\sigma_2+a_3\sigma_3$ kaikki kertoimet $a_0,a_1,a_2,a_3$ ovat reaalilukuja. Tällaisessa tilanteessa käytämme merkintää $\mathbf{a}=(a_1,a_2,a_3)\in\mathbb{R}^3$ ja kirjoitamme $A=a_0I+\mathbf{a}\cdot\mathbf\sigma$, missä $\mathbf{a}\cdot\mathbf\sigma=a_1\sigma_1+a_2\sigma_2+a_3\sigma_3$.
Tärkeän luokan itseadjungoituja matriiseja muodostavat positiiviset matriisit, $A\geq 0$, eli matriisit, joille sisätulo $\left\langle{\psi}|{A\psi}\right\rangle\geq 0$ kaikilla vektoreilla $\psi=(z,w)\in\mathbb{C}^2$. Pienellä laskulla todetaan, että matriisi $A$ on positiivinen, jos ja vain jos $a_0\geq 0, -a_0\leq a_3\leq a_0$, ja $A$:n determinantti ${\rm det}[A]=a_{11}a_{22}-a_{21}a_{12}=$$(a_0+a_3)(a_0-a_3)-(a_1+ia_2)(a_1-ia_2)\geq 0$ eli $a_0^2\geq a_1^2+a_2^2+a_3^2=\left\|{\mathbf{a}}\right\|^2$. Matriisin $A$ jälki $\mathrm{tr}\left[A\right]$, eli sen diagonaalialkioiden summa, $\mathrm{tr}\left[A\right]=a_{11}+a_{22}=2a_0$, on myös tärkeä käsite.
3.1 Tilat
Spin-$\frac 12$-objektin tilajoukko (spintilat, polarisaatiotilat, kubittitilat) koostuu sellaisista $A\in M(\mathbb{C}^2)$, jotka ovat positiivisia, $A\geq 0$, ja joiden jälki on yksi, $\mathrm{tr}\left[{A}\right]=1$. Käytämme tilajoukolle nyt merkintää $\boldsymbol{S}(\mathbb{C}^2)$ ja tiloille kreikkalaista kirjainta $\rho$ (mahdollisesti alaindeksillä täsmennettynä). Kun määritellään $\boldsymbol{n}=2\boldsymbol{a}$, huomataan, että yllä annetuin merkinnöin tila $\rho\in\mathbf S(\mathbb{C}^2)$ voidaan lausua muodossa
| (3.1) | $\rho=\rho_{\mathbf{n}}= \frac 12( I+\boldsymbol{n}\cdot\boldsymbol{\sigma}) = \frac 12 \left(\begin{matrix} 1+n_3&n_1-\imath\,n_2\\ n_1+\imath\,n_2&1-n_3 \end{matrix}\right),$ |
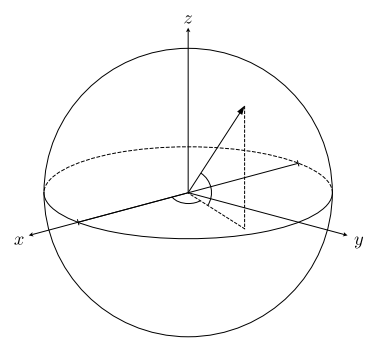
missä $\boldsymbol{n}=(n_1,n_2,n_3)$ on vektori, jonka pituus $\left\|\boldsymbol{n}\right\|\leq 1$. Koska $\rho_{\boldsymbol{n}}=\rho_{\boldsymbol{m}}$, jos ja vain jos vektorit $\boldsymbol{n}$ ja $\boldsymbol{m}$ ovat samat, $\boldsymbol{n}=\boldsymbol{m}$, niin huomaamme, että spin-$\frac 12$-objektin tilajoukko $\boldsymbol S(\mathbb{C}^2)$ vastaa kääntäen yksikäsitteisesti kolmiulotteisen reaalisen vektoriavaruuden $\mathbb{R}^3$ yksikköpallon $\boldsymbol{S}(\mathbb{R}^3)=\{\boldsymbol{n}\in\mathbb{R}^3|\, \left\|{\boldsymbol{n}}\right\|\leq 1\}$ pisteitä. Tilajoukko on konveksi, ja sen ääripisteet (puhtaat tilat) saadaan tarkalleen kyseisen yksikköpallon ääripisteinä eli sen pinnan pisteinä, siis vektoreilla $\boldsymbol{n}$, joiden pituus $\left\|{\boldsymbol{n}}\right\|=1$. Helposti todetaan, että $\rho_n$ on puhdas, jos ja vain jos $\rho_{\boldsymbol{n}}$ on idenpotentti, $\rho_n^2=\rho_n$. Jos tila ei ole puhdas, niin se on sekoitettu: jos $0\ne \left\|\boldsymbol{n}\right\| <1$, niin kirjoittamalla $\hat{\boldsymbol{n}}=\boldsymbol{n}/{\left\|\boldsymbol{n}\right\|}$ saamme $\rho=\lambda\rho_{\hat{\boldsymbol{n}}}+(1-\lambda)\rho_{-\hat{\boldsymbol{n}}}$, missä $\lambda=\frac 12(1+\left\|\boldsymbol{n}\right\|)$. Käytämme yleisesti merkintää $\hat{\boldsymbol{a}}$ sen korostamiseksi, että tämä $\mathbb{R}^3$:n vektori $(a_1,a_2,a_3)$ on yksikkövektori.
Taustatietoa 3. Olkoon $(z,w)\in\mathbb{C}^2$ yksikkövektori, $|z|^2+|w|^2=1$. Sen avulla määritelty matriisi [16] $\left(\begin{matrix} |z|^2& \bar wz\\ \bar zw &|w|^2 \end{matrix}\right)$ on puhdas tila, ja jos
| $ \left(\begin{matrix} |z|^2&\bar wz\\ \bar zw &|w|^2 \end{matrix}\right)=\left(\begin{matrix} |u|^2&\bar vu\\ \bar uv &|v|^2 \end{matrix}\right),$ |
niin yksikkövektorit $(z,w)$ ja $(u,v)$ eroavat toisistaan vain ns. vaihetekijällä, ts. $(z,w)=\lambda(u,v)$ jollekin $\lambda\in\mathbb{C}, |\lambda|=1$. Tämän johdosta Hilbertin avaruuden yksikkövektoreita käytetään usein puhtaiden tilojen edustajina. Tällöin on kuitenkin muistettava, että vaihetekijällä eroavat yksikkövektorit edustavat samaa puhdasta tilaa. Esimerkiksi yksikkövektori $(\sqrt{\frac 12(1+n_3)},\frac 12(n_1+in_2)/\sqrt{\frac 12(1+n_3)})$ on eräs puhtaan tilan $\rho_n=\frac 12(I+\boldsymbol{n}\cdot\boldsymbol{\sigma}), \left\|\boldsymbol{n}\right\|=1$, edustaja. [17]
3.2 Suureet ja todennäköisyydet
Kun tilajoukko $\boldsymbol{S}(\mathbb{C}^2)$ on kiinnitetty, niin sen konveksi rakenne yhdessä tilastollisen kausaliteetin vaatimuksen kanssa johtaa sekä suureiden $O$ että todennäköisyysmittojen $p^O_\rho$ rakenteen täydelliseen määräytymiseen. [18]
Spin-$\frac 12$-systeemien, kuten kaikkien kaksitasosysteemien, tapauksessa on luonnollista tarkastella ns. kaksiarvoisia suureita (muitakin tietysti on, mutta tässä riittää tämä), joiden arvojoukoiksi voidaan valita kahden pisteen joukko, esimerkiksi $\Omega =\{-1,1\}$, jolloin mahdolliset testijoukot ovat tyhjä joukko $\emptyset$, koko joukko $\Omega$, sekä yksiöt $\{\pm 1\}$. Tällaisen suureen matemaattiseksi esitykseksi saadaan kaksiarvoinen operaattorifunktio, ns. operaattorimitta $\{\pm 1\}\mapsto \mathsf{E}(\{\pm 1\})=E_\pm$, missä $E_\pm$ on (positiivinen) matriisi, ns. efektioperaattori,
| (3.2) | $E_+ = \frac 12(e_0 I+ \boldsymbol{e}\cdot\boldsymbol{\sigma}),$ |
| (3.3) | $ E_-=I-E_+= \frac 12[(2-e_0) I- \boldsymbol{e}\cdot\boldsymbol{\sigma}],$ |
jossa (todennäköisyysehdon $0\leq p^O_\rho(\{\pm 1\}) \leq 1$, $\rho\in\mathbf S(\mathbb{C}^2)$, johdosta) $\left\|{\boldsymbol{e}}\right\|\leq\min\{e_0,2-e_0\}$, ja siis $0\leq e_0\leq 2$ ja $\left\|\boldsymbol{e}\right\|\leq 1$. Suureen $\mathsf{E}$ mittaustulostodennäköisyydet $p^\mathsf{E}_\rho(\{\pm 1\})$ tilassa $\rho=\rho_{\boldsymbol{n}}$ ovat nyt välttämättä muotoa
| (3.4) | $ p^\mathsf{E}_\rho(\{\pm 1\})=\mathrm{tr}[{\rho_{\boldsymbol{n}} E_\pm }]= \begin{cases} \frac 12(e_0+ \boldsymbol{n}\cdot\boldsymbol{e}) \\ \frac 12[(2-e_0)-\boldsymbol{n}\cdot\boldsymbol{e}] \end{cases}, $ |
missä $\mathbb{R}^3$:n vektoreiden $\boldsymbol{n}=(n_1,n_2,n_3)$ ja $\boldsymbol{e}=(e_1,e_2,e_3)$ (euklidinen) sisätulo $\boldsymbol{n}\cdot\boldsymbol{e}=$$n_1e_1+n_2e_2+n_3e_3=$$\left\|\boldsymbol{n}\right\|\left\|\boldsymbol{e}\right\|\cos(\theta_{\boldsymbol{n},\boldsymbol{e}})$, missä $\cos(\theta_{\boldsymbol{n},\boldsymbol{e}})$ on vektoreiden $\boldsymbol{n}$ ja $\boldsymbol{e}$ välisen kulman $\theta_{\boldsymbol{n},\boldsymbol{e}}$ kosini.
Tilojen joukossa puhtaat tilat erottuvat ehdolla $\rho_n^2=\rho_n$, eli $\left\|\boldsymbol{n}\right\|=1$. Samalla tavalla suureiden $\mathsf{E}$ joukosta erottuvat ne, joille $e_0=\left\|\boldsymbol{e}\right\|=1$. Suoralla laskulla voidaan varmistaa, että myös näin on tarkalleen silloin kun $E_\pm^2=E_\pm$, eli efektit ovat ns. projektio-operaattoreita. [19] Tällaisen suureen $\mathsf{E}$ efektit $E_\pm$ ovat siis projektioita ja ne määräävät yksikäsitteisen itseadjungoidun operaattorin $A=1\cdot E_+ + (-1)\cdot E_-=\boldsymbol{e}\cdot\boldsymbol{\sigma}$, missä vektori $\boldsymbol{e}$ on siis yksikkövektori.
Taustatietoa 4. Koska itseadjungoidun operaattorin $A\in M(\mathbb{C}^2)$ yleinen muoto on $A=a_0+\boldsymbol{a}\cdot\boldsymbol{\sigma}$, niin huomaamme, että näin saatiin vain osa itseadjungoiduista operaattoreista, muotoa $\boldsymbol{a}\cdot\boldsymbol{\sigma}$, $\left\|\boldsymbol{a}\right\|=1$, olevat operaattorit. Helposti todetaan, että jokainen reaalilukupari $(a,b)\in\mathbb{R}^2$ määrittelee projektioiden $E_\pm$ kanssa samalla tavalla yksikäsitteisen itseadjungoidun operaattorin
| $A=aE_++bE_-=\frac 12(a+b) I+\frac 12(a-b)\boldsymbol{e}\cdot\boldsymbol{\sigma}, \quad \left\|\boldsymbol{e}\right\| =1,$ |
joka on muotoa $A=a_0+\boldsymbol{a}\cdot\boldsymbol{\sigma}$, kun $a_0=\frac 12(a+b), \boldsymbol{a}=\frac 12(a-b)\boldsymbol{e}$. Tämä itseadjungoitu operaattori syntyy projektioarvoisesta suureesta $\mathsf{E}$, jonka mahdolliset mittaustulokset, operaattorin $A$ ominaisarvot, ovat nyt $a$ ja $b$, ts. $\Omega=\{a,b\}$, ja epätriviaalit testijoukot ovat yksiöt $\{a\}$ ja $\{b\}$. Suureen $\mathsf{E}$ mittaustulostodennäköisyydet ovat lausekkeen (3.4) mukaisesti $p^\mathsf{E}_{\rho_\boldsymbol{n}}(\{a\})=\frac 12(1+\boldsymbol{n}\cdot\boldsymbol{e})$ ja $p^\mathsf{E}_{\rho_{\boldsymbol{n}}}(\{b\})=\frac 12(1-\boldsymbol{n}\cdot\boldsymbol{e})$, missä $\left\|\boldsymbol{n}\right\|\leq 1$ ja $\left\|\boldsymbol{e}\right\|=1$. [20]
Itseadjungoidun operaattorin esitystä $A=a_0I+\boldsymbol{a}\cdot\boldsymbol{\sigma}$ vastaten kirjoitamme sen spektraalihajotelman usein muodossa
| $A= (a_0+\left\|\boldsymbol{a}\right\|)P_{\hat{\boldsymbol{a}}}+(a_0-\left\|\boldsymbol{a}\right\|)P_{-\hat{\boldsymbol{a}}}, \quad P_{\pm\hat{\boldsymbol{a}}}=\frac 12(I\pm\hat{\boldsymbol{a}}\cdot\boldsymbol{\sigma}), \quad \hat{\boldsymbol{a}}=\boldsymbol{a}/\left\|\boldsymbol{a}\right\|,$ |
sen korostamiseksi että hajotelma on $A$:n (yksikäsitteinen) spektraalihajotelma eli että efektit $P_{\pm\hat{\boldsymbol{a}}}$ ovat projektioita ja $P_{-\hat{\boldsymbol{a}}}=I-P_{\hat{\boldsymbol{a}}}$. Tällä hajotelmalla on erityisiä ominaisuuksia kuten se, että operaattorin $A$ neliö $A^2$ (kuten kaikki muutkin sen potenssit) saadaan suoraan neliöimällä (korottamalla potenssiin) hajotelman kertoimet: $A^2= (a_0+\left\|\boldsymbol{a}\right\|)^2P_{\hat{\boldsymbol{a}}}+(a_0-\left\|\boldsymbol{a}\right\|)^2P_{-\hat{\boldsymbol{a}}}$. [21]
Luonnollisesti mitkä tahansa kaksi efektiä $E$ ja $F$ määrittelevät jokaisella reaalilukuparilla $(a,b)$ myös itseadjungoidun operaattorin $A=aE+bF$. Kysymyksessä ei kuitenkaan ole $A$:n spektraalihajotelma ellei $E$ ole projektio ja $F=I-E$. Jos $F=I-E$, niin $E$ ja $F$ määrittelevät kaksiarvoisen suureen, esimerkiksi $a$ ja $b$ mahdollisina mittaustuloksinaan. Tämä suure ei kuitenkaan liity operaattoriin $A=aE+bF$ muussa kuin keskiarvomielessä, ellei $E$ ja siis myös $F=I-E$ ole projektio, vrt. Luku 2.
3.3 Kaksi von Neumannin tulosta
Von Neumannin laajan työn kaksi keskeistä tulosta kvanttimekaniikan perusrakenteen selkeyttämiseksi olivat itseadjungoitujen operaattoreiden spektraalirakenteen selvittäminen sekä keskenään kommutoivien itseadjungoitujen operaattoreiden karakteroisointi. Nämä merkittävät matemaattiset tulokset määrittivät pitkälle teorian voittokulkua erilaisten fysikaalisten ilmiöiden kuvaamisessa samalla kuitenkin sementoiden vuosikymmenten ajaksi sen käsitteellisen perustan tarpeettoman ahtaaksi.
Kvanttimekaniikan alkuaikojen muotoiluissa fysikaaliselle suureelle haluttiin löytää yksittäinen operaattoriesitys, siis suureen $O$ esitys, jossa kaikki sen mittaustulostodennäköisyydet $p^O_s(X)$ voidaan rekonstruoida yhdestä (suuretta edustavasta) operaattorista. Tämän ongelman von Neumannin ratkaisi osoittamalla, että jokainen Hilbertin avaruuden itseadjungoitu operaattori syntyy jostakin yksikäsitteisestä projektioarvoisesta mitasta, spektraalimitasta, ja jokainen tällainen suure määrittelee erään yksikäsitteisen itseadjungoidun operaattorin.
Vaatimus fysikaalisen suureen esittämisestä yhdellä operaattorilla merkitsi kuitenkin voimakasta idealisoivaa rajoitusta teorian puitteissa kuvattavissa oleville mittauksille sulkien pois ison joukon luonnollisia reaalistisia mittauskonteksteja. Tällaisia (projektioarvoisia) suureita kutsutaan tarkoiksi suureiksi. Muita suureita kutsutaan usein sumeiksi suureiksi (vaikka ne eivät teknisessä mielessä välttämättä olisikaan tarkkojen suureiden sumennoksia). Fysikaalisen suureen esitys operaattorina on elänyt sitkeänä kvanttimekaniikan opetusperinteessä.
Toinen, jo mainittu, von Neumannin tärkeä tulos koskee fysikaalisten suureiden samanaikaista mitattavuutta: kaksi itseadjungoituna operaattorina esitettävää suuretta on mitattavissa yhdessä, jos ja vain jos nämä operaattorit kommutoivat keskenään.
Suoralla laskulla todetaan, että itseadjungoidut operaattorit $A=a_0I+\boldsymbol{a}\cdot\boldsymbol{\sigma}$ ja $B=b_0I+\boldsymbol{b}\cdot\boldsymbol{\sigma}$ toteuttavat ”vaihtorelaation”
| $AB= BA + 2\imath (\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{\sigma},$ |
missä $\boldsymbol{a}\times\boldsymbol{b}$ on vektoreiden $\boldsymbol{a}$ ja $\boldsymbol{b}$ ristitulo, siis vektori, joka on kohtisuorassa vektoreiden $\boldsymbol{a}$ ja $\boldsymbol{b}$ määrittelemää tasoa vastaan ja jonka pituus on $\left\|\boldsymbol{a}\right\|\left\|\boldsymbol{b}\right\||\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|$. Huomaamme että $AB=BA$, jos ja vain jos $\boldsymbol{a}\times\boldsymbol{b}=0$, eli vektoreiden suunnat ovat samat tai vastakkaiset, merk. $\boldsymbol{a}\parallel\boldsymbol{b}$. [22] Niinpä mitään kahta eri (itseadjugoiduilla operaattoreilla esitettävää, ns. tarkkaa) spinsuuretta $A$ ja $B$, $\boldsymbol{a}\not\parallel\boldsymbol{b}$, ei voida mitata yhdessä. [23] Saamme luvussa 6 nähdä, että keskenään epäkommutatiivisten muotoa (3.2) olevien efektien $E=\frac 12(e_oI+\boldsymbol{e}\cdot\boldsymbol{\sigma})$ ja $F=\frac 12(f_oI+\boldsymbol{f}\cdot\boldsymbol{\sigma})$ määrittelemät kaksiarvoiset (sumeat) suureet voivat olla mitattavissa yhdessä, kunhan lukuneliköt $(e_0,\boldsymbol{e})$ ja $(f_0,\boldsymbol{f})$ toteuttavat sopivat ehdot.
Esimerkki 4. Tarkkaa spinsuuretta $A=\hat{\boldsymbol{a}}\cdot\boldsymbol{\sigma}$ kusutaan spiniksi suunnassa $\hat{\boldsymbol{a}}$. Matriisit $\sigma_1,\sigma_2,\sigma_3$ ovat tässä puhetavassa spinit koordinaattiakselien $x,y$ ja $z$ suunnissa. Helposti nähdään, että nämä kolme suuretta (itseadjungoitua operaattoria) liittyvät kolmeen eri (spin, polarissaatio, tai kubitti)kantaan $\{\frac 1{\sqrt 2}(1,1),\frac 1{\sqrt 2}(1,-1)\}$, $\{\frac 1{\sqrt 2}(1,i),\frac 1{\sqrt 2}(1,-i)\}$, ja $\{(1,0),(0,1)\}$, vastaavasti. Esimerkiksi ensimmäisen kannan vektorit $\frac 1{\sqrt 2}(1,1)$ ja $\frac 1{\sqrt 2}(1,-1)$ määrittelevät projektiot (vrt. Taustatietoa 3)
| $P_{\hat x}= \frac 12 \left(\begin{matrix} 1&1\\ 1 &1\end{matrix}\right) \quad{\rm ja}\quad P_{-\hat x}=\frac 12\left(\begin{matrix} 1&-1\\ -1 &1 \end{matrix}\right),$ |
jotka antavat hajotelman $\sigma_1= P_{\hat x} – P_{-\hat x}$, josta nähdään, että suureen $\sigma_1$ mahdolliset mittaustulokset ovat $\pm 1$ ja niiden todennäköisyydet tilassa $\rho_n$ ovat $p^{\sigma_1}_{\rho_n}(\{\pm 1\})=\mathrm{tr}[{\rho_n P_{\pm\hat x}}]=\frac 12(1\pm n_1)$.
4. Kvanttimekaniikan aito todennäköisyysluonne
Vaikka kvanttimekaniikan puhtaat tilat ja (itseadjungoituina operaattoreina kuvattavissa olevat) tarkat suureet vastaavat täysin klassisen mekaniikan vastaavia idealisaatioita, niin teorian todennäköisyysluonne on nyt täysin toinen. Tämä nähdään helposti jo yksinkertaisella esimerkillämme. Suureen $A =(a_0+\left\|\boldsymbol{a}\right\|)P_{\hat{\boldsymbol{a}}}+(a_0-\left\|\boldsymbol{a}\right\|)P_{-\hat{\boldsymbol{a}}}$ mittaustulostodennäköisyydet puhtaassa tilassa $\rho_n, \left\|\boldsymbol{n}\right\|=1$, ovat $\frac 12(1\pm \cos\theta_{\boldsymbol{n},\hat{\boldsymbol{a}}})$. Mutta $\frac 12(1\pm \cos\theta_{\boldsymbol{n},\hat{\boldsymbol{a}}})\in\{0,1\}$ jos ja vain jos $ \cos\theta_{\boldsymbol{n},\hat{\boldsymbol{a}}}=\pm 1$ eli kun vektorien $\boldsymbol{n}$ ja $\boldsymbol{a}$ suunnat ovat samat tai vastakkaiset, $\boldsymbol{n}\parallel\boldsymbol{a}$, siis oleellisesti vain kun $A$ on spin suunnassa $\boldsymbol{n}$. Jos vektorit $\boldsymbol{n}$ ja $\boldsymbol{a}$ ovat keskenään kohtisuorassa, $\boldsymbol{n}\perp\boldsymbol{a}$, niin molemmat todennäköisyydet ovat $\frac 12$. [24]
Suureen $A$ mahdollisten mittaustulosten $a_0\pm\left\|\boldsymbol{a}\right\|$ todennäköisyysteoreettinen keskiarvo ja varianssi (hajonnan neliö) tilassa $\rho_{\boldsymbol{n}}$ (puhdas tai sekoitettu) ovat nyt [25]
\begin{eqnarray*} \langle A\rangle_\rho &=& (a_0+\left\|\boldsymbol{a}\right\|) p^A_{\rho_{\boldsymbol{n}}}(\{a_0+\left\|\boldsymbol{a}\right\|\})+ (a_0-\left\|\boldsymbol{a}\right\|) p^A_{\rho_{\boldsymbol{n}}}(\{a_0-\left\|\boldsymbol{a}\right\|\}) \\ &=& a_0+\boldsymbol{a}\cdot\boldsymbol{n}= a_0+\left\|\boldsymbol{a}\right\|\left\|\boldsymbol{n}\right\|\cos\theta_{\boldsymbol{n},\boldsymbol{a}}=_{{}_{\left\|\boldsymbol{n}\right\|=1}} a_0+\left\|\boldsymbol{a}\right\|\cos\theta_{\boldsymbol{n} ,\boldsymbol{a}}, \\ {\rm Var}_{\rho_{\boldsymbol{n} }}(A)&=& (a_0+\left\|\boldsymbol{a}\right\|)^2 p^A_{\rho_{\boldsymbol{n}}}(\{a_0+\left\|\boldsymbol{a}\right\|\})+ (a_0-\left\|\boldsymbol{a}\right\|)^2 p^A_{\rho_{\boldsymbol{n}}}(\{a_0-\left\|\boldsymbol{a}\right\|\}) – \ (a_0+\boldsymbol{a}\cdot\boldsymbol{n})^2\\ &=& {\left\|\boldsymbol{a}\right\|}^2-(\boldsymbol{a}\cdot\boldsymbol{n})^2 = {\left\|\boldsymbol{a}\right\|}^2(1-{\left\|\boldsymbol{n}\right\|}^2\cos^2\theta_{\boldsymbol{n},\boldsymbol{a}}) =_{{}_{\left\|\boldsymbol{n}\right\|=1}} {\left\|\boldsymbol{a}\right\|}^2(1-\cos^2\theta_{\boldsymbol{n},\boldsymbol{a}}). \end{eqnarray*}
Tässä on kolme huomionarvoista asiaa:
| a) | tarkan suureen $A$ mittaustulostodennäköisyydet tilassa $\rho_{\boldsymbol{n} }$ ovat aitoja, $\ne 0,1$, paitsi kun tila on puhdas ja $\boldsymbol{n} \parallel\boldsymbol{a}$, |
| b) | suureen $A$ mittaustulosten keskiarvo tilassa $\rho_{\boldsymbol{n} }$ ei ole mahdollinen mittaustulos, paitsi kun tila on puhdas ja $\boldsymbol{n} \parallel\boldsymbol{a}$, |
| c) | suureen $A$ hajonta tilassa $\rho_{\boldsymbol{n} }$ on aidosti positiivinen, paitsi kun tila on puhdas ja $\boldsymbol{n} \parallel\boldsymbol{a}$. |
Nämä perustavat tulokset kyseenalaistavat sen klassisesta fysiikasta tutun ajatuksen, että fysikaalisella suureella, kuten paikka tai energia, olisi aina, siis kaikissa tiloissa, hyvin määritelty, mahdollisesti tuntematon arvo, jonka mittaus sitten paljastaisi. Mahdolliset mittaustulokset toki tiedetään, mutta (esimerkiksi) ehtoa $0\ne p^A_{\rho_{\boldsymbol{n}}}(\{a_0\pm\left\|\boldsymbol{a}\right\|\})\ne 1$ ei voida suoraviivaisesti tulkita niin, että suureella $A$ olisi tilassa $\rho_{\boldsymbol{n}}$ jompi kumpi näistä (mittaustulos)arvoista $a_0\pm\left\|\boldsymbol{a}\right\|$, mutta emme vain tiedä kumpi. Kvanttimekaniikan mittausteorian kehittely osoittaa lisäksi, ettei mittauksen jälkeenkään voida välttämättä sanoa, että mitatulla suureella olisi mittaustuloksen osoittama arvo. Kvanttimekaniikassa fysikaalisen suureen arvoista puhuminen vaatii erityistä huolellisuutta. Vain tilanteessa, jossa jonkin suureen mahdollinen mittaustulos voidaan ennustaa (probabilistisella) varmuudella, voidaan tällaista realistista puhetapaa käyttää ongelmitta. Esimerkiksi jos spinsysteemi on puhtaassa tilassa $\rho_{\hat{\boldsymbol{a}}}$, jolloin tarkan suureen $A$ mittaustulostodennäköisyys arvolle $a_0+\left\|\boldsymbol{a}\right\|$ on 1 ja arvolle $a_0-\left\|\boldsymbol{a}\right\|$ se on 0, niin tällaista realistista puhetapaa voi käyttää.
Toinen huomion arvoinen seikka on, että suureen $A$ mittaustulosjakauman $p^A_{\rho_{\boldsymbol{n}}}$ leveyttä, esimerkiksi hajontaa $\Delta_{\rho_{\boldsymbol{n}}}(A)=\sqrt{{\rm Var}_{\rho_{\boldsymbol{n}}}(A)}$, ei myöskään voida suoraviivaisesti tulkita mittausvirheeksi, suureen mittausepätarkkuudeksi; nollasta eroava hajonta ei ole hajontaa suureen ”oikean arvon” ympärillä. Kvanttimekaniikassa yksittäisellä mittaustuloksella (ja suureen arvoista puhumisella) ei juuri ole merkitystä, mittaustulos on koko mittaustulostilasto.
Esimerkki 5. Arkinen kolikonheitto voidaan helposti pukea myös kaksiarvoisen probabilistisen kokeen muotoon, mahdollisina tuloksina kruuna ja klaava, joille voidaan käyttää esimerkiksi lukuja 1 ja -1, tai vaikkapa 1 ja 0. Tasapainoisella rahalla suoritetulle rehdille heitolle annamme kummallekin tulokselle saman todennäköisyyden $\frac 12$. Kolikkoa voidaan toki heittää monelle eri tavalla, esimerkiksi niin, että varmuudella saadaan kruuna. Näitä eri heittotapoja, heiton alustuksia, voidaan kuvata kolikonheiton tiloina, tilajoukkona $\mathbf S(2)=\{\lambda s_1+(1-\lambda)s_2\,|\, 0\leq \lambda \leq 1\}$, missä $s_1$, vast. $s_2$, on heittotapa (tila) joka tuottaa varmuudella tuloksen kruuna, vast. klaava. Tilassa $s=\lambda s_1+(1-\lambda)s_2$ suoritettu kolikonheitto tuottaa tulokset kruuna ja klaava todennäköisyyksillä $s(\{kruuna\})= \lambda s_1(\{kruuna\})+(1-\lambda)s_2(\{kruuna\})=\lambda$ ja $s(\{klaava\})=1-\lambda$.
Jokainen spinsuure, kuten esimerkiksi $\sigma_1=P_{\hat x}-P_{- \hat x}$ (tarkka) spin suunnassa $x$, on myös kaksiarvoinen suure, jonka mahdollisina mittaustuloksina ovat 1 (kruuna) ja -1 (klaava). Dramaattinen ero on nyt tilajoukoissa $\boldsymbol{S}(2)$ ja $\boldsymbol{S}(\mathbb{C}^2)$. Klassisessa tilajoukossa $\boldsymbol{S}(2)$ on tarkalleen 2 puhdasta tilaa, $s_1$ ja $s_2$, ja kaikki muut tilat $s\in\boldsymbol{S}(2)$ ovat näiden yksikäsitteisiä konveksikombinaatioita. Puhtaassa tilassa $s_1$ kruunan todennäköisyys on 1 ja klaavan 0. Kvanttitilajoukko $\boldsymbol{S}(\mathbb{C}^2)$ puolestaan sisältää kontinuumin verran eri puhtaita tiloja $\rho_{\hat{\boldsymbol{n}}}, \hat n\in\mathbb{R}^3, \left\|\boldsymbol{n}\right\|=1$, ja jokainen sekoitettu tila $\rho_{\boldsymbol{n}}, \left\|\boldsymbol{n}\right\|<1,$ voidaan lausua ylinumeroituvalla tavalla eri puhtaiden tilojen konveksikombinaationa. Spinsuureeseen $\sigma_1$ liittyen tilajoukossa $\boldsymbol{S}(\mathbb{C}^2)$ toki on kaksi erityistä puhdasta tilaa, nimittäin $\rho_{\hat{\boldsymbol{n}}}, \hat{\boldsymbol{n}}=(1,0,0)$, ja $\rho_{-\hat{\boldsymbol{n}}}$, sekä niiden seokset $\lambda\rho_{\hat{\boldsymbol{n}}}+(1-\lambda)\rho_{-\hat{\boldsymbol{n}}}$. Nämä tilat vastaavat suureelle $\sigma_1$ tilajoukkoa $\mathbf S(2)$ mutta $\sigma_1$-mittausten mahdollisten (jopa puhtaiden) preparointien joukko on huikeasti laajempi. Puhtaassa tilassa $\rho_{\hat{\boldsymbol{n}}}$ $\sigma_1$-mittauksen `kruunan’ todennäköisyys on $\frac 12(1+n_1)$, joka on 1 vain jos $\hat n=(1,0,0)$. Tilajoukossa $\mathbf S(2)$ ei ole lainkaan puhtaiden tilojen $s_1$ ja $s_2$ superpositioita, kun taas tilajoukossa $\boldsymbol{S}(\mathbb{C}^2)$ jokainen puhdas tila $\rho_{\hat{\boldsymbol{n}}}, \rho_{\hat{\boldsymbol{n}}}\ne\rho_{\pm\hat x}$, voidaan lausua puhtaiden tilojen $\rho_{\pm\hat x}$ superpositioina, [26] vastaten juuri sitä, että missä tahansa puhtaassa tilassa $\rho_{\hat{\boldsymbol{n}}}$, $\hat{\boldsymbol{n}}\ne\pm(1,0,0)$, suureen $\sigma_1$ mittaustulostodennäköisyydet ovat aitoja. Geometrisesti ’jana’ $\boldsymbol{S}(2)$ voidaan nähdän `pallon’ $\boldsymbol{S}(\mathbb{C}^2)$ minä tahansa lävistäjänä, esimerkiksi juuri janana $[(-1,0,0),(1,0,0)]$, ks. Kuva 5.
5. Epäkommutatiivisuus ja kysymys energiasummasta $H=T+V$
Klassisessa mekaniikassa esimerkiksi massapisteen kokonaisenergia on tyypillisesti muotoa $H=T+V$, liike-energian ja potentiaalienergian summa. Tämä on myös kvanttimekaanisen systeemin (tarkan) energiasuureen tyypillinen rakenne. Esimerkiksi vetyatomin energia voidaan lausua itseadjungoituna operaattorina, joka on juuri tällaista muotoa. Klassisessa mekaniikassa energia voidaan mitata (tai määrittää laskemalla annetuista alkuehdoista) mittaamalla (tai laskemalla) erikseen sekä liike-energia että potentiaalienergia ja laskemalla tulokset yhteen. Myös kvanttimekaniikassa sekä liike-energia $T$ että potentiaalienergia $V$ voidaan periaatteessa mitata erikseen missä tahansa systeemin tilassa. Näin ei kuitenkaan saada energialle mittaustulosta eikä mittaustulostilastoa. Suureet $T$ ja $V$ (itseadjungoituina operaattoreina) eivät kommutoi keskenään, joten niitä ei voida mitata yhdessä. Energian $H$ mittaus on toteutettava riippumattomasti, se ei ole $T$:n ja $V$:n yhteismittaus. Koska kuitenkin $H=T+V$, niin tilastollisen keskiarvon mielessä toki saadaan
| $\langle H\rangle_\rho =\langle T\rangle_\rho+\langle V\rangle_\rho.$ |
Toisin sanoen vaikka mitään suurepareista $(H,T), (H,V), (T,V)$ ei voida mitata yhdessä, niin näiden suureiden mittaustulostilastot $p^H_\rho, p^T_\rho,p^V_\rho$ kytkeytyvät toisiinsa keskiarvojensa $\langle H\rangle_\rho, \langle T\rangle_\rho, \langle V\rangle_\rho$ kautta yllä kuvatulla tavalla.
Tätä tärkeää tulosta voidaan taas havainnollistaa esimerkillä. Olkoot $A=\boldsymbol{a}\cdot\boldsymbol{\sigma}$ ja $B=\boldsymbol{b}\cdot\boldsymbol{\sigma}$ kaksi tarkkaa spinsuuretta, $\boldsymbol{a}\ne\pm\boldsymbol{b}, \left\|\boldsymbol{a}\right\|=\left\|\boldsymbol{b}\right\|=1$. Tällöin myös $A+B=(\boldsymbol{a}+\boldsymbol{b})\cdot\boldsymbol{\sigma}$ on tarkka spinsuure. Koska $A$ ja $B$ eivät kommutoi keskenään, niin niitä ei voi mitata yhdessä. Kaikki kolme suuretta voidaan kuitenkin mitata erikseen missä tahansa tilassa $\rho_{\boldsymbol{n}}$ tilastojen (jakaumien) $p^A_{\rho_{\boldsymbol{n}}}, p^B_{\rho_{\boldsymbol{n}}}$ ja $p^{A+B}_{\rho_{\boldsymbol{n}}}$ määrittämiseksi. Mittaustulostodennäköisyydet ovat nyt kaikki muotoa $\frac 12(1\pm\boldsymbol{n}\cdot\boldsymbol{c})$, missä $\boldsymbol{c}$ on tapauskohtaisesti jokin vektoreista $\boldsymbol{a},\boldsymbol{b},\boldsymbol{a}+\boldsymbol{b}$. Silti $\langle A\rangle_{\rho_{\boldsymbol{n}}}+\langle B\rangle_{\rho_{\boldsymbol{n}}}=\langle A+B\rangle_{\rho_{\boldsymbol{n}}}$ kaikilla $\rho_{\boldsymbol{n}}$. Huomaa, että suureen $A+B$ mahdolliset mittaustulokset ovat $\pm\left\|\boldsymbol{a}+\boldsymbol{b}\right\|$, kun taas suureiden $A$ ja $B$ mahdolliset mittaustulokset ovat $\pm\left\|\boldsymbol{a}\right\|$ ja $\pm\left\|\boldsymbol{b}\right\|$.
6. Epäkommutatiivisuus vs. yhteismitattavuus
Itseadjungoituina operaattoreina esitettävät suureet ovat mitattavissa yhdessä, jos ja vain jos niitä edustavat operaattorit kommutoivat. Kun fysikaalisen suureen matemaattinen esitys laajennetaan itseadjungoidusta operaattorista, sen spektraalimitasta, efektiarvoiseksi mitaksi, niin yhteys kommutatiivisuuden ja yhteismitattavuuden väliltä katoaa: kommutatiivisuus on riittävä muttei välttämätön ehto yhteismitattavuudelle. Havainnollistamme tätä tärkeää seikkaa taas muotoa (3.2) olevilla kaksiarvoisilla suureilla $\mathsf{E}$ ja $\mathsf{F}$ olettamalla yksinkertaisuuden vuoksi, että
| $E_\pm=\frac 12(I\pm\boldsymbol{e}\cdot\boldsymbol{\sigma}), \qquad F_\pm=\frac 12(I\pm\boldsymbol{f}\cdot\boldsymbol{\sigma}),$ |
siis, että $e_0=f_0=1$. Nämä sumeat suureet $\mathsf{E}$ ja $\mathsf{F}$, $\mathsf{E}(\{\pm 1\})= E_\pm$, $\mathsf{F}(\{\pm 1\})= F_\pm$, ovat keskenään epäkommutatiivisia, $[E_i,F_j]\ne 0$, kaikilla $i,j=\pm$, aina kun $\boldsymbol{e}\not\parallel\boldsymbol{f}$. Kysymys näiden suureiden yhteismitattavuudesta palautuu nyt siihen, voidaanko löytää sellainen suure $\mathsf{G}$ ja funktiot $f$ ja $g$, että ehto (2.1) toteutuu. On selvää, että tällaisella suureella täytyy olla neljä mahdollista mittaustulosta vastaten tulospareja $(1,1), (-1,1), (1,-1), (-1,-1)$, vrt. esimerkki 2. Valitaan neljä eri reaalilukua $a,b,c,d$, joita voidaan merkitä myös symboleilla $++,-+,+-,-$$-$. Tällöin luonnolliset asteikkofunktiot $f$ ja $g$ ovat esimerkiksi
| $f(a)=f(c)=1, f(b)= f(d)=-1 \quad{\rm ja\ siis\ esim.}\quad f^{-1}(\{1\})=\{a,c\},\\ g(a)=g(b)=1, g(c)=g(d)=-1\quad{\rm ja\ siis\ esim.}\quad g^{-1}(\{-1\})=\{c,d\}.$ |
Ehdon (2.1) mukaisesti pitäisi nyt olla [27]
| $E_+ =\mathsf{G}(\{a,c\})=\mathsf{G}(\{a\})+\mathsf{G}(\{c\})=G_{++}+G_{+-}\\$ $E_-=\mathsf{G}(\{b,d\})=\mathsf{G}(\{b\})+\mathsf{G}(\{d\})=G_{-+}+G_{- -}\\$ $F_+=\mathsf{G}(\{a,b\})=\mathsf{G}(\{a\})+\mathsf{G}(\{b\})=G_{++}+G_{-+}\\$ $F_-=\mathsf{G}(\{c,d\})=\mathsf{G}(\{c\})+\mathsf{G}(\{d\})=G_{+-}+G_{- -}.$ |
Suoralla laskulla voidaan osoittaa, että annetut ehdot toteutuvat, ja siis $\mathsf{E}$ ja $\mathsf{F} $ ovat yhteismitattavissa, tarkalleen silloin kun vektorit $\boldsymbol{e}$ ja $\boldsymbol{f}$ toteuttavat seuraavan geometrisen ehdon: [28]
| $ \left\|{\boldsymbol{e}+\boldsymbol{f}}\right\|+\left\|{\boldsymbol{e}-\boldsymbol{f}}\right\|\leq 2.$ |
Jos näin on, niin efekteiksi $G_{ij}, i,j\in\{+,-\}$, voidaan valita
| $G_{ij}= \frac 14[(1+ij\boldsymbol{e}\cdot\boldsymbol{f})I+(i\boldsymbol{e}+j\boldsymbol{f})\cdot\boldsymbol{\sigma}].$ |
Tämä tulos avaa myös mahdollisuuden tutkia kahden keskenään epäkommutatiivisen suureen approksimatiivista yhteismitattavuutta käyttäen tarkkojen suureiden, esimerkiksi $A$ ja $B$, approksimaattoreina sumeita yhdessä mitattavissa olevia suureita $\mathsf{E}$ ja $\mathsf{F} $. Palaamme tähän luvussa 10.
Esimerkki 6. Tarkastellaan konkreettisena esimerkkinä tarkkojen spinsuureiden $\sigma_i=\frac 12(I+\sigma_i)-\frac 12(I-\sigma_i), i=1,2$, sumennoksia $\mathsf{E}$ ja $\mathsf{F}$, joiden efektit ovat $\frac 12(I\pm \lambda_i\sigma_i),0\leq \lambda_i\leq 1, i=1,2$, vektoreina $\boldsymbol{e}=(\lambda_1,0,0)$ ja $\boldsymbol{f}=(0,\lambda_2,0)$. Suureet $\mathsf{E}$ ja $\mathsf{F}$ ovat nyt yhteismitattavissa tarkalleen silloin, kun $\sqrt{\lambda_1^2+\lambda_2^2}\leq 1$, esimerkiksi kun $\lambda_1=\lambda_2=0.7$. Tässä tapauksessa suureiden $\mathsf{E}$ ja $\mathsf{F}$ yhteismittauksen toteuttaa esimerkiksi suure $\mathsf{G}$ efektein $G_{ij}=\frac 14(I+i\lambda_1\sigma_1+j\lambda_2\sigma_2), i,j=\pm 1$.
7. Mittauksen aiheuttama häiriö
Luku $p^\mathsf{E}_\rho(X)$ on todennäköisyys sille, että suureen $\mathsf{E}$ mittaus tilassa $\rho$ tuottaa tuloksen joukosta $X$. Tässä mittaustapahtumalle ei aseteta mitään erityisvaatimuksia, mittaus voi jopa tuhota mitattavan systeemin tuloksen rekisteröinnin yhteydessä, esimerkiksi elektronin tai fotonin iskeytyessä havaintolevylle tai fotodetektoriin. Mikä tahansa suure voidaan kuitenkin mitata, ainakin periaatteessa, niin että systeemi ei tässä tuhoudu ja on vielä käytössä uutta mittausta varten. Mittaus kuitenkin yleensä vaikuttaa systeemiin, ja tämä vaikutus ilmenee mittaustulosjakaumissa $p^\mathsf{E}_\rho$, niiden muuntumisina. Näiden todennäköisyysmittojen rakenteen johdosta kaikki systeemin kokemat muutokset voidaan ilmaista joko tilojen muuntumisina $\rho\mapsto\hat m(\rho)$ tai suureiden muuntumisina $\mathsf{E}\mapsto \tilde m(\mathsf{E})$ niin, että $p^\mathsf{E}_{\hat m(\rho)}=p^{\tilde m(\mathsf{E})}_\rho$ kaikilla $\rho$ ja $\mathsf{E}$. Mittausten tapauksessa voimme tutkia erityisesti ehdollisia muuntumisia, esimerkiksi tilan muuntumista ehdolla, että suureen $\mathsf{E}$ mittaus $m$ tilassa $\rho$ tuottaa tuloksen joukosta $X\in\mathcal{A}$, $\rho\mapsto \hat m_X(\rho)$. Tällaisen ehdollisen muunnoksen avulla voimme laskea esimerkiksi todennäköisyyden sille, että suureen $\mathsf{F}$ mittaus tuottaa tuloksen joukosta $Y$, ehdolla, että ensin suoritettu suureen $\mathsf{E}$ mittaus $m$ tilassa $\rho$ tuottaa tuloksen joukosta $X$. Näin saatavat ehdolliset todennäköisyydet, kaksoistodennäköisyydet $(X,Y)\mapsto \mathrm{tr}[{\hat m_X(\rho)\mathsf{E}(Y)}]=\mathrm{tr}[{\rho\tilde m_X(\mathsf{E}(Y))}]$, $\rho\in\mathbf S$, määrittelevät ns. kaksoissuureen, mahdollisina mittaustuloksina tulosparit, jossa ensimmäinen osasuure on ensin mitattu suure $\mathsf{E}$ ja toinen osasuure toiseksi mitatun suureen muunnos, sumennos $\tilde{\mathsf{F}}=\tilde{m}_{\Omega}(\mathsf{F})$. Menemättä teorian matemaattisiin yksityiskohtiin toteamme vain, että jos ensin mitattu suure $\mathsf{E}$ on tarkka (projektioarvoinen), niin muuntunut suure $\tilde{\mathsf{F}}$ välttämättä kommutoi sen kanssa, siis $\mathsf{E}(X)\tilde{\mathsf{F}}(Y)=\tilde{\mathsf{F}}(Y)\mathsf{E}(X)$ kaikilla testijoukoilla $X$ ja $Y$.
Tarkastellaan esimerkkinä kahden tarkan spinsuureen $A$ ja $B$ jonomittausta, esimerkiksi niin, että ensin suoritetaan suureen $A$ mittaus. Suure $B=b_0I+\boldsymbol{b}\cdot\boldsymbol{\sigma}=(b_0+\left\|\boldsymbol{b}\right\|)P_{\hat{\boldsymbol{b}}}+ (b_0-\left\|\boldsymbol{b}\right\|)P_{-\hat{\boldsymbol{b}}}$ muuntuu tämän mittauksen johdosta suureeksi, jonka määrittelemät efektit $\tilde P_{\pm\hat{\boldsymbol{b}}}$ kommutoivat $A$:n kanssa. Jokainen $\mathbb{C}^2$-mallin efekti on muotoa $F=\frac 12(f_0I+\boldsymbol{f}\cdot\boldsymbol{\sigma})$, ja se kommutoi $A$:n kanssa tarkalleen silloin, kun $\boldsymbol{a}\times\boldsymbol{f}=0$, siis kun $\boldsymbol{f}\parallel\boldsymbol{a}$. Olkoon $\boldsymbol{f}=f\hat{\boldsymbol{a}},|f|\leq 1$, jolloin $\tilde P_{\hat{\boldsymbol{b}}}=\frac 12(f_0I+f\hat{\boldsymbol{a}}\cdot\boldsymbol{\sigma})$ ja $\tilde B_{-\hat{\boldsymbol{b}}}=\frac 12[(2- f_0)I-f\hat{\boldsymbol{a}}\cdot\boldsymbol{\sigma}]$. Vakiot $f_0$ ja $f$ riippuvat mittauksen yksityiskohdista. Esimerkiksi suureen $A$ ns. Lüdersin mittauksessa $B$:n efektit, projektiot $P_{\pm\hat{\boldsymbol{b}}}$, muuntuvat efekteiksi $\tilde P_{\pm\hat{\boldsymbol{b}}}=P_{\hat{\boldsymbol{a}}}P_{\pm\hat{\boldsymbol{b}}}P_{\hat{\boldsymbol{a}}}+P_{-\hat{\boldsymbol{a}}}P_{\pm\hat{\boldsymbol{b}}}P_{-\hat{\boldsymbol{a}}}$, josta saadaan pienellä laskulla $f_0=1$ ja $f=\hat{\boldsymbol{a}}\cdot\hat{\boldsymbol{b}}=\cos\theta_{\boldsymbol{a},\boldsymbol{b}}$.
Tarkan suureen $A$ mittauksen vaikutuksesta tarkka suure $B$ on muuntunut sumeaksi suureeksi, jonka efektit $\tilde P_{\pm\hat{\boldsymbol{b}}}$ riippuvat suureesta $A$, sen suuntavektorista $\boldsymbol{a}$; riippuvuus suureesta $B$ on kutistunut kertoimiin $f_0,f$. Suureen $B$ kaikki keskeiset määrittelyominaisuudet (symmetriaominaisuudet) ovat tuhoutuneet tässä suureen $A$ mittauksessa täysin riippumatta siitä, miten A mitattiin.
Samalla tavalla esimerkiksi ensin paikan $Q$ mittaus ja sitten liikemäärän $P$ mittaus johtaa aina siihen, että liikemäärä $P$ muuntuu sumeaksi paikkasuureeksi ja liikemäärän symmetriaominaisuudet ovat täysin tuhoutuneet.
8. Mittaus(epä)tarkkuus
Todennäköisyydet $p^\mathsf{E}_\rho, \mathsf{E}\in\boldsymbol{O}$, määräävät systeemin tilan $\rho$, sen miten systeemi on preparoitu, ja ne yhdessä ovat näin ensisijaisesti preparoinnin (tilan) ominaisuus. Yksittäisen mittaustulosjakauman mahdollinen leveys ei kuvaa tämän suureen mittaustarkkuutta tässä tilassa. Suure $\mathsf{E}$, tarkka tai sumea, määräytyy täysin jakaumista $p^\mathsf{E}_\rho, \rho\in\boldsymbol{S}$. Suureen mahdollinen epätarkka mittaus ilmenee siinä, että tosiasiassa suoritetun mittauksen mittaustulosjakaumat poikkeavat mitattavaksi aiotun suureen jakaumista. Kvanttimekaniikassa mittausvirhe/tarkkuus on siis perustettava mitattavaksi aiotun suureen, maalisuureen $\mathsf{E}$, ja tosiasiassa mitatun suureen, approksimaattorin $\mathsf{M}$, mittaustulosjakaumien $p^\mathsf{E}_\rho$ ja $p^\mathsf{M}_\rho$, $\rho\in\boldsymbol{S}$, vertailulle.
Mittausvirheelle voidaan asettaa eräitä luonnollisia ehtoja. Ensinnäkin mittausvirheen laadun, esim. metri, tulisi olla sama kuin mitattavan suureen laatu. Toiseksi, jos mittakaavaa muutetaan, esimerkiksi metrit senttimetreiksi, niin virheen tulisi skaalautua vastaavasti. Suureen mittausvirhe on luonnollista valita myös tilariippumattomaksi, sillä mikä tahansa suure tai suurepari voidaan annetussa tilassa mitata niin, että virhettä ei synny.
Olkoon $\Delta(p^\mathsf{M}_\rho,p^\mathsf{E}_\rho)$ jokin dimensio- ja skaalausehdon toteuttava todennäköisyysmittojen $p^\mathsf{M}_\rho$ ja $p^\mathsf{E}_\rho$ vertailuun käytetty positiivinen funktio. Funktion pienin yläraja
| $ \Delta(\mathsf{M},\mathsf{E})=\sup_{\rho} \Delta(p^\mathsf{M}_\rho,p^\mathsf{E}_\rho)$ |
on yksi mahdollinen virhe sille, kun maalisuure $\mathsf{E}$ mitataan mittauksella, joka tosiasiassa määrittelee suureen $\mathsf{M}$. Tässä lähestymistavassa mittausvirhe on siis korkeintaan $\Delta(\mathsf{M},\mathsf{E})$.
Todennäköisyyslaskenta, erityisesti optimaalisen kuljetuksen (optimal transport) teoria, tuntee monia yllä mainitut ehdot toteuttavia funktioita. Yksi tunnetuimmista on Gaspard Mongen (1746-1818) aikoinaan optimaaliseen maan siirtoon kehittämä menetelmä, joka antaa valittujen kriteerien mukaan edullisimman tavan siirtää alueesta $\Omega$ maakasa jakaumalla $p$ alueeseen $\Xi$ jakaumalla $q$.
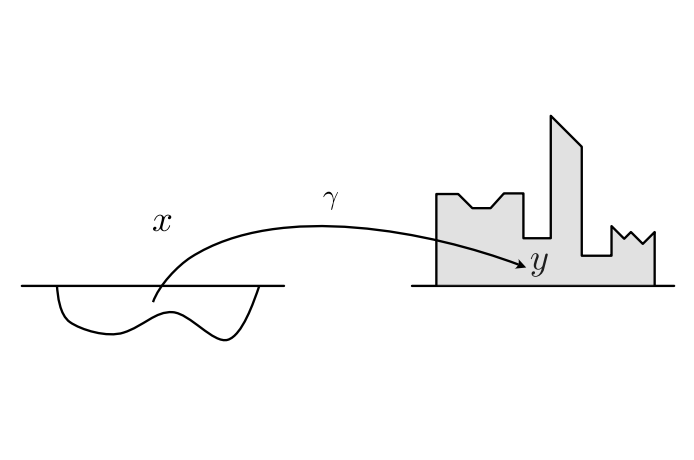
Tässä osakuorman siirtämiskustannus kohdasta $x\in \Omega$ kohtaan $y\in \Xi$ riippuu suoraan etäisyydestä $|x-y|$ ja siitä, miten jakauma $p$ muokataan jakaumaksi $q$. Todennäköisyysteoreettisesti tämä jakaumien yhdistäminen mallinnetaan todennäköisyysmittojen $p$ ja $q$ kytkennällä, kaksoistodennäköisyysmitalla $\gamma$, jonka osa- eli marginaalitodennäköisyyksinä [29] $p$ ja $q$ saadaan, jolloin tämän yhdistämistavan ja valitun kustannusfunktion mukainen siirron kokonaishinta on
| $\Delta_1^\gamma(q,p)=\int |x-y|d\,\gamma(x,y).$ |
Optimoitu hinta saadaan, kun valitaan kytkentä, joka minimoi hinnan, ts. $\Delta_1(p,q)= \inf_\gamma\Delta_1^\gamma(p,q)= \min_\gamma\Delta_1^\gamma(p,q)$. [30] Tässä voidaan käyttää erilaisia kustannusfunktioita $(x,y)\mapsto c(x,y)$, esimerkiksi etäisyyden neliötä $|x-y|^2$, joka vastaa tilannetta, jossa todennäköisyysmitan leveyttä mitataan varianssilla tai sen neliöjuurella, hajonnalla.
Jokainen kustannusfunktio $c$ tuottaa erään luonnollisen virhemitan kuvaamaan mitatun suureen $\mathsf{M}$ poikkeamaa maalisuureesta $\mathsf{E}$,
| $\Delta_c(\mathsf{M} ,\mathsf{E})=\sup_\rho\Delta_c(p^\mathsf{M} _\rho,p^\mathsf{E}_\rho)=\sup_\rho\inf_\gamma\Delta_c^\gamma(p^\mathsf{M} _\rho,p^\mathsf{E}_\rho).$ |
Usein käytetty kustannusfunktio on etäisyyden neliö, joka antaa 2. kertaluvun metrisen virheen, Wassersteinin 2. kertaluvun virheen, $\Delta_2(\mathsf{M},\mathsf{E})$. Vaikka virhe $\Delta_2$ on käsitteellisesti melko yksinkertainen, sen konkreettinen laskeminen vaatii useimmiten syvällistä matematiikkaa. Menemättä yleiseen teoriaan todettakoon kuitenkin, että hyvin yleisillä kustannusfunktioilla, erityisesti kaikilla metrisillä funktioilla pätee: jos $\Delta_c(\mathsf{M},\mathsf{E})=0$, niin $\mathsf{M}=\mathsf{E}$.
Spiniä koskevassa esimerkkitapauksessamme mittausvirheet, kuten $\Delta_2(\mathsf{M},\mathsf{E})$, voidaan suoraviivaisesti laskea. Tilanteessa jossa kummankin suureen mahdolliset mittaustulokset ovat $\pm 1$, maalisuure on tarkka suure $A=\hat{\boldsymbol{a}} \cdot\mathbf\sigma=P_{\hat{\boldsymbol{a}} }-P_{-\hat{\boldsymbol{a}} }$, $P_{\pm\hat{\boldsymbol{a}} }=\frac 12(I\pm\hat{\boldsymbol{a}} \cdot\mathbf\sigma)$, ja suureen $\mathsf{M}$ efektit ovat $M_+=\frac 12(m_0I+\boldsymbol{m}\cdot\boldsymbol{\sigma}), M_-=I-M_+$, tulokseksi saadaan
| $ \Delta_2(\mathsf{M},A)^2= 2(|m_0-1|+\left\|{\boldsymbol{m}}-\hat{\boldsymbol{a}}\right\|).$ |
Tästä myös suoraan nähdään, että jos $\Delta_2(\mathsf{M},\mathsf{E})=0$, niin $m_0=1$ ja $\boldsymbol{m}=\hat{\boldsymbol{a}}$, eli suureet ovat samat.
Taustatietoa 5. Kahden kaksiarvoisen todennäköisyysmitan, kuten $p^A_\rho$ ja $p^\mathsf{M}_\rho$, kaikki kytkennät $\gamma$, yhdistetyt todennäköisyydet, on helppo määrittää. Esimerkistä 2 nähdään, että jos $p^A_\rho(\{1\})=p$ ja $p^\mathsf{M}_\rho(\{1\})=q$, niin $\gamma$ määräytyy neljästä positiiviluvusta $\gamma(\{(1,1)\})=r, \gamma(\{1,-1\})=p-r,\gamma(\{-1,1\})=q-r$, ja $\gamma(\{-1,-1\})=1-p-q+r$, jolloin $\Delta_2^\gamma(p^\mathsf{M}_\rho,p^A_\rho)^2=4(p+q-2r)$ ja siis
$\Delta_2(p^\mathsf{M}_\rho,p^A_\rho)^2=\min_\gamma\Delta_2^\gamma(p^A_\rho,p^\mathsf{M}_\rho)^2=4|p-q|=2|1-m_0+\boldsymbol{n}\cdot(\hat{\boldsymbol{a}}-\boldsymbol{m})|$,
kun $\rho=\rho_{\boldsymbol{n}}$. Tästä saadaan
$\Delta_2(\mathsf{M},A)^2=\max_{\boldsymbol{n}}2|1-m_0+\boldsymbol{n}\cdot(\hat{\boldsymbol{a}}-\boldsymbol{m})|=2(|m_0-1|+\left\|{\boldsymbol{m}-\hat{\boldsymbol{a}}}\right\|)$.
Olkoon $\mathsf{M}$ vakio, siis suure jonka mittaustulostodennäköisyydet eivät riipu tilasta. Tällöin välttämättä $M_+=mI$ ja $M_-=(1-m)I$, jollekin $0\leq m\leq 1$. Tällöin $\Delta_2(\mathsf{M},A)^2=2(|1-2m|+1)\in[2,4]$, erityisesti virheen $\Delta_2(\mathsf{M},A)$ maksimi on siis 2.
Esimerkki 7. Tarkan spinsuureen $\sigma_1=\frac 12(I+\sigma_1)-\frac 12(I-\sigma_1)$ approksimointi sumealla spinsuureella $\mathsf{E}$, efekteinä $\frac 12(I\pm\lambda_1\sigma_1)$, johtaa mittausvirheeseen $\Delta_2(\mathsf{E},\sigma_1)=\sqrt{2(1-\lambda_1)}\in[0,\sqrt 2]$; esimerkiksi arvolla $\lambda_1=0,7$ virhe $\simeq 0,77$.
Esimerkki 8. Tarkastellaan jonomittauksen ”ensin $A$, sitten $B$” aiheuttamaa häirötä, kun $B$ muuntuu suureeksi $\tilde B$, efektein $\tilde B_\pm =\frac 12(I\pm\cos\theta_{\boldsymbol{a},\boldsymbol{b}}\hat{\boldsymbol{a}}\cdot\boldsymbol{\sigma})$, ks. luku 7. Tällöin $\Delta_2(\tilde{B}{,}B)=$$\sqrt{2\left\|\cos\theta_{\boldsymbol{a},\boldsymbol{b}}\hat{\boldsymbol{a}}-\hat{\boldsymbol{b}}\right\|}=$$\sqrt{2|\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|}.$ Odotusten mukaisesti häiriö on suurimmillaan, kun $\hat{\boldsymbol{a}}\perp\hat{\boldsymbol{b}}$
9. Preparointiepätarkkuusrelaatiot
Tarkastellaan asiaa taas esimerkkimme kautta. Suureen $A=a_0I+\boldsymbol{a}\cdot\boldsymbol{\sigma}=$$(a_0+\left\|\boldsymbol{a}\right\|)P_{\hat{\boldsymbol{a}}}+(a_0-\left\|\boldsymbol{a}\right\|)P_{-\hat{\boldsymbol{a}}}$ mittaustulostodennäköisyydet tilassa $\rho_n$ ovat $\mathrm{tr}[{\rho_n P_{\pm\hat{\boldsymbol{a}}}}]=\frac 12(1\pm\boldsymbol{n}\cdot\hat{\boldsymbol{a}})$. Todennäköisyysjakauman leveyttä voidaan kuvata monella tavalla, esimerkiksi neliöllisellä keskipoikkeamalla, varianssilla, tai sen neliöjuurella, hajonnalla,
| $ {\rm Var}_{\rho_n}(A)= {\left\|\boldsymbol{a}\right\|}^2[1-(\boldsymbol{n}\cdot\hat{\boldsymbol{a}})^2] \,,\quad{\rm tai}\quad \Delta_{\rho_n}(A)=\sqrt{{\rm Var}_{\rho_n}(A)}.$ |
Huomaamme, että sopivalla tilan valinnalla mittaustulosten hajonta saadaan nollaksi. Olkoon $B=b_0I+\boldsymbol{b}\cdot\boldsymbol{\sigma}$ jokin toinen tarkka suure ja $\Delta_{\rho_n}(B)$ sen mittaustuloshajonta tilassa $\rho_n$. Jos suureet $A$ ja $B$ eivät kommutoi keskenään, niin systeemiä ei voida valmistaa sellaiseen tilaan, jossa molempien suureiden $A$ ja $B$ mittaustuloshajonnat olisivat nollia: jos $\Delta_{\rho_n}(A)=0$, niin $\Delta_{\rho_n}(B)\ne 0$ ja jos $\Delta_{\rho_n}(B)=0$, niin $\Delta_{\rho_n}(A)\ne0$.
Tässä ilmenevää suureiden $A$ ja $B$ mittaustulosjakaumien toisiinsa kytketymistä kuvaa suorimmin niiden preparointiepätarkkuusalue, kuten esimerkiksi
| $ \mathsf{PUR}(A,B)=\{(\Delta_{\rho_n}(A),\Delta_{\rho_n}(B))\,|\, \rho_n\in\mathbf S(\mathbb{C}^2)\}.$[31] |
Tämä on tason $\mathbb{R}^2$ positiivisen neljänneksen $\mathbb{R}^+\times\mathbb{R}^+$, esimerkissämme suorakaiteen $[0,\left\|\boldsymbol{a}\right\|]\times[0,\left\|\boldsymbol{b}\right\|]$, alue. Jos $A$ ja $B$ eivät kommutoi keskenään, niin origo $(0,0)\notin\mathsf{PUR}(A,B)$. Suureiden $A$ ja $B$ (preparointi-) epätarkkuusrelaatiolla tarkoitetaan tyypillisesti juuri niiden hajontoja $\Delta_{\rho_n}(A)$ ja $\Delta_{\rho_n}(B)$ koskevaa epäyhtälöä, joka ilmaisee sen, että molemmat näistä eivät voi olla samassa tilassa `pieniä’ eli että on olemassa jokin origon $(0,0)$ ympäristö, joka ei sisälly joukkoon $\mathsf{PUR}(A,B)$.
Tarkasteltavassa yksinkertaisessa esimerkkitapauksessa tutulla tulomuotoisella epäyhtälöllä ei ole merkitystä, sillä se antaa nyt vain itsestään selvän tuloksen: $\Delta_{\rho_n}(A)\Delta_{\rho_n}(B)\geq 0$. Sen sijaan tässä on luonnollista käyttää additiivisia (summaa rajoittavia) epäyhtälöitä. Tapauksessa $\left\|\boldsymbol{a}\right\|=\left\|\boldsymbol{b}\right\|=1$ hajonnoille saadaan tulos
| (9.1) | $\Delta_{\rho_n}(A)+\Delta_{\rho_n}(B)\geq \left\|{\boldsymbol{n}\times\boldsymbol{a}}\right\|+\left\|{\boldsymbol{n}\times\boldsymbol{b}}\right\|\geq \left\|{\boldsymbol{a}\times\boldsymbol{b}}\right\| =|\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|. $ |
Epäyhtälön suurempi alaraja on tilariippuva, ja siinä on yhtäsuuruus kun tila on puhdas, $\left\|\boldsymbol{n}\right\|=1$. Se on pienimmillään kun $\boldsymbol{n}=\pm\boldsymbol{a}$ tai $\boldsymbol{n}=\pm\boldsymbol{b}$. Jälkimmäinen tilasta riippumaton alaraja `mittaa’ suureiden epäkommutatiivisuuden astetta (lukuna väliltä $[0,1]$), ja se ilmaisee sen, että epätarkkuusalue $\mathsf{PUR}(A,B)$ on suoran $d_1+d_2=|\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|, (d_1,d_2)\in\mathbb{R}^2$, yläpuolella. Jos $\boldsymbol{a}\parallel\boldsymbol{b}$, eli $A$ ja $B$ kommutoivat keskenään, niin tämä alaraja on nolla ja se saavutetaan kun tila on puhdas ja $\boldsymbol{n}\parallel\boldsymbol{a}$. Toinen ääripää esiintyy kohtisuorien spinsuuureiden ($\boldsymbol{a}\perp\boldsymbol{b}$) tapauksessa, jolloin alaraja on 1. Päätepisteitään lukuunottamatta jana $\{\lambda(1,0)+(1-\lambda)(0,1)=(\lambda,1-\lambda)\,|\, 0\leq \lambda \leq 1\}$ ei kuitenkaan kuulu joukkoon $\mathsf{PUR}(A,B)$. Se rajaa aluetta alhaalta mutta ei ole sen reuna.
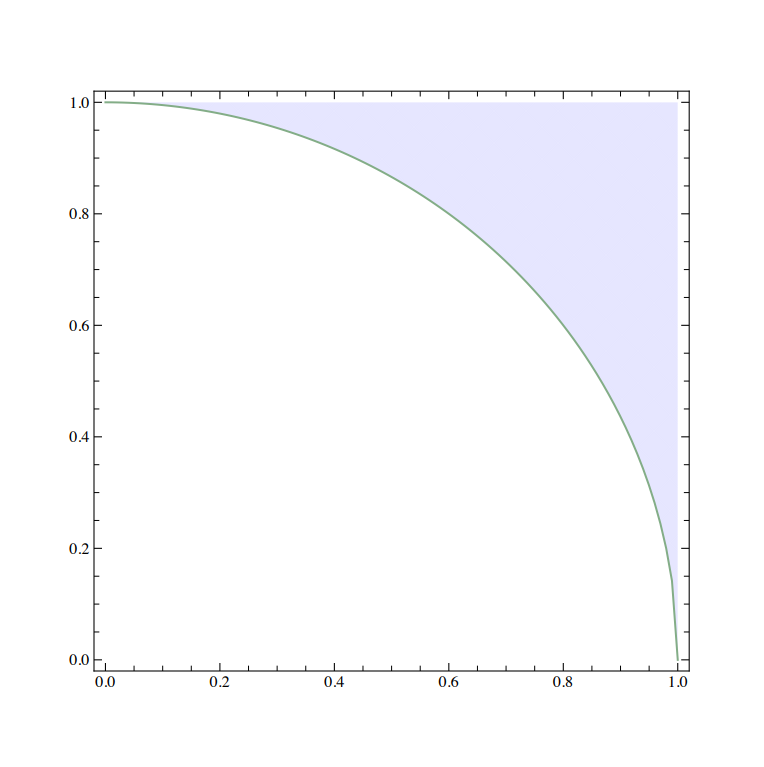
Esimerkki 9. Tarkastellaan konkreettisena esimerkkinä vektoreihin $\boldsymbol{a}=(1,0,0)$ ja $\boldsymbol{b}=(0,1,0)$ liittyviä spinsuureita $A=\sigma_1$ ja $B=\sigma_2$. Hajontojen määrittelemä preparointiepätarkkuusalue on nyt
| $ \mathsf{PUR}(A,B)=\{(\sqrt{1-n_1^2},\sqrt{1-n_2^2})\,|\, (n_1,n_2)\in\mathbb{R}^2, n_1^2+n_2^2\leq 1\}. $ |
Tämä on origokeskisen yksikköympyrän komplementti tason positiivisen neljänneksen suorakaiteessa $[0,1]\times[0,1]$ ja epätarkkuusalueen alareuna (ympyrän kaari) saavutetaan kun $\rho_n=\frac 12(I+n_1\sigma_1+n_2\sigma_2)$, ts. $\boldsymbol{n}=(n_1,n_2,0), n_1^2+n_2^2=1$.
*****
Paikan ja liikemäärän epätarkkuusrelaatiot ovat jopa maallikoille tuttu, ja niiden tutkimus juontuu jo Heisenbergin vuoden 1927 työhön. Voidaan osoittaa, että paikan ja liikemäärän preparointiepätarkkuusalue $\mathsf{PUR}(Q,P)=\{(\Delta_\rho(Q),\Delta_\rho(P))\,|\, \rho\in\mathbf S(H)\}$ koostuu $\mathbb{R}^2$:n positiivisen neljänneksen $[0,\infty)\times[0,\infty)$ suorakulmaisista hyperbeleistä $\Delta_\rho(Q)\Delta_\rho(P)=\ {\rm vakio} \ \geq \frac{\hbar}2$, mukaan lukien reunahyperbeli $\Delta_\rho(Q)\Delta_\rho(P)=\frac\hbar{2}$; [32] jokaista lukua $c\geq \frac 12$ kohti on olemassa parvi tiloja $\rho_c$ niin että koko hyberbeli $\Delta_{\rho_c}(Q)\Delta_{\rho_c}(P)=c\hbar$ saavutetaan. [33] Alue $\mathsf{PUR}(Q,P)$ yhtyy kuvan 9 alueeseen $\mathsf{MUR}(Q,P)$.
10. Mittausepätarkkuusrelaatiot
Olkoot $A=\hat{\boldsymbol{a}}\cdot\mathbf\sigma$ ja $B=\hat{\boldsymbol{b}}\cdot\mathbf\sigma$ kaksi tarkkaa spinsuuretta. Niitä ei voida mitata yhdessä (kun $\boldsymbol{a}\not\parallel\boldsymbol{b}$). Lukujen 6 ja 8 nojalla ne voidaan kuitenkin mitata yhdessä likimääräisesti, esimerkiksi virhein $\Delta_2(\mathsf{M},A)$ ja $\Delta_2(\mathsf{M}’,B)$, aina kun niitä approksimoivat suureet $\mathsf{M}$ ja $\mathsf{M}’$ ovat yhteismitattavissa. [34] Suureiden $A$ ja $B$ mittausepätarkkuusalue $\mathsf{MUR}(A,B)$ määritellään, analogisesti niiden preparointiepätarkkuusalueen $\mathsf{PUR}(A,B)$ kanssa, esimerkiksi joukkona [35] \begin{eqnarray*} \mathsf{MUR}(A,B)&=&\{(\Delta_2(\mathsf{M},A),\Delta_2(\mathsf{M}’,B))\,|\, \mathsf{M},\mathsf{M}’\ {\rm yhteismitattavissa}\,\}\\ &=&\{(\sqrt{ 2(|m_0-1|+\left\|{\boldsymbol{m}-\hat{\boldsymbol{a}}}\right\|)},\sqrt{ 2(|m_0′-1|+\left\|{\boldsymbol{m}’-\hat{\boldsymbol{b}}}\right\|)})\,|\, \mathsf{M},\mathsf{M}’\ {\rm yhteismitattavissa}\,\}. \end{eqnarray*}
Tämä alue sisältyy tason positiivisen neljänneksen joukkoon $[0,2]\times[0,2]$. Sen tyhjentävä määrittäminen on melko laaja tehtävä. [36] Seuraavaan kohtaan on kerätty joitakin sen pääkohtia ja sitä seuraavassa esimerkissä on kuvattu alue $\mathsf{MUR}(\sigma_1,\sigma_2)$.
Taustatietoa 6. Kun $\hat{\boldsymbol{a}}\not\parallel\hat{\boldsymbol{b}}$, niin piste $(0,0)$ ei voi kuulua joukkoon $\mathsf{MUR}(A,B)$, sillä jos näin olisi, niin $\mathsf{M}=A$ ja $\mathsf{M}’=B$, jolloin myös $A$ ja $B$ olisivat yhteismitattavissa, ja siis $\hat{\boldsymbol{a}}\parallel\hat{\boldsymbol{b}}$. Sen sijaan, toinen virheistä voi nyt olla nolla. Jos esim. $\Delta_2(\mathsf{M},A)=0$, niin $\mathsf{M}= A$. Koska $\mathsf{M}$, ja siis $A$, voidaan mitata yhdessä suureen $\mathsf{M}’$ kanssa, niin $\mathsf{M}’$ välttämättä kommutoi $A$:n kanssa. Tällöin $\boldsymbol{m}’\times\hat{\boldsymbol{a}}=0$ ja siis $M’_+=\frac 12(m_0’I+\boldsymbol{a}\cdot\mathbf\sigma)$, jollekin $\boldsymbol{a}=a\hat{\boldsymbol{a}}, |a|\leq 1$ (vrt. Luku 7). Niinpä
$\Delta_2(\mathsf{M}’,B)^2=$$2(|m_0′-1|+\left\|{\boldsymbol{a}-\hat{\boldsymbol{b}}}\right\|)$$\geq 2\sqrt{\left\|{\boldsymbol{a}}\right\|^2+1-2\left\|{\boldsymbol{a}}\right\|\cos\theta_{\boldsymbol{a},\boldsymbol{b}}}$$\geq 2|\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|$,
ja alaraja saavutetaan kun $\mathsf{M}’$ valitaan niin, että $a=\cos\theta_{\boldsymbol{a},\boldsymbol{b}}$ (vrt. Esimerkki 8). Siksi janat $[(0,\sqrt{2|\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|}), (0,\sqrt 2)]$ ja $[(\sqrt{2|\sin\theta_{\boldsymbol{a},\boldsymbol{b}}|},0), (\sqrt 2,0)]$ kuuluvat alueeseen $\mathsf{MUR}(A,B)$ (vrt. Esimerkki 7).
Jos $\mathsf{M}$ ja $\mathsf{M}’$ valitaan vakiosuureiksi $M_+=mI, M_+’=m’I$, missä $0\leq m,m’\leq 1$, niin virheet $\Delta_2(\mathsf{M},A)=\sqrt{2(2-m)}$ ja $\Delta_2(\mathsf{M}’,B)=\sqrt{2(2-m’)}$ täyttävät alueen $[0,2]\times[0,2]\setminus[0,\sqrt 2)\times[0,\sqrt 2)$. Lisäksi voidaan osoittaa, että alueen $[0,\sqrt 2]\times[0,\sqrt 2]$ sisältämät yhteismittausvirheet voidaan kaikki saavuttaa efektien $M_\pm=\frac 12(I\pm\boldsymbol{m}\cdot\mathbf\sigma)$ ja $M_\pm’=\frac 12(I\pm\boldsymbol{m}’\cdot\mathbf\sigma)$ määrittelemillä suureilla kun $\left\|{\boldsymbol{m}+\boldsymbol{m}’}\right\|+\left\|{\boldsymbol{m}-\boldsymbol{m}’}\right\|\leq 2$ (yhteismittauskriteeri) ja vektorit $\boldsymbol{m}$ ja $\boldsymbol{m}’$ ovat vektoreiden $\hat{\boldsymbol{a}}$ ja $\hat{\boldsymbol{b}}$ määrittelemässä tasossa. Seuraavassa esimerkissä tämä alue määritetään kun $A=\sigma_1$ ja $B=\sigma_2$, jolloin $\hat{\boldsymbol{a}}=(1,0,0)$ ja $\hat{\boldsymbol{b}}=(0,1,0)$ ovat keskenään kohtisuorat.
Esimerkki 10. Tarkastellaan tapausta $A=\frac 12(I+\sigma_1)-\frac 12(I-\sigma_1)$ ja $B=\frac 12(I+\sigma_2)-\frac 12(I-\sigma_2)$. Edeltävän kohdan mukaan kaikki pisteet $(d_1,d_2)\in[0,2]\times[0,2]\setminus[0,\sqrt 2)\times[0,\sqrt 2)$ kuuluvat alueeseen $\mathsf{MUR}(\sigma_1,\sigma_2)$. Lisäksi suureiden $\sigma_1$ ja $\sigma_2$ likimääräiset yhteismittaukset, virhein $(d_1,d_2)\in\mathsf{MUR}(\sigma_1,\sigma_2)\cap [0,\sqrt 2]\times[0,\sqrt 2]$, voidaan toteuttaa efektien $M_\pm=\frac 12(I\pm(m_1\sigma_1+m_2\sigma_2))$ ja $M_\pm’=\frac 12(I\pm(m_1’\sigma_1+m_2’\sigma_2))$ määrittelemillä suureilla kunhan vektorit $\boldsymbol{m}=(m_1,m_2,0)$ ja $\boldsymbol{m}’=(m_1′,m_2′,0)$ toteuttavat ehdon $\left\|{(m_1+m_1′,m_2+m_2′,0)}\right\|+\left\|{(m_1-m_1′,m_2-m_2′,0)}\right\|\leq 2$. Koska suunnat $\hat{\boldsymbol{a}}=(1,0,0)$ ja $\hat{\boldsymbol{b}}=(0,1,0)$ ovat keskenään kohtisuoruorassa, niin tilanne yksinkertaistuu vielä tästäkin. Voidaan osoittaa, että tässä tapauksessa riittää tarkastella suureiden $\sigma_1$ ja $\sigma_2$ sumennoksia, siis suureita joille $M_\pm=\frac 12(I+c\sigma_1)$ ja $M_\pm’=\frac 12(I+d\sigma_2)$, $c^2+d^2\leq 1$. Tällöin $\Delta_2(\mathsf{M},A)^2=2(1-c)$ ja $\Delta_2(\mathsf{M}’,B)^2=2(1-d)$, ja siis
$\mathsf{MUR}(\sigma_1,\sigma_2)\cap [0,\sqrt 2]\times[0,\sqrt 2]=\{(\sqrt{2(1-c)},\sqrt{2(1-d)})\,|\, c^2+d^2\leq 1\}$.
Kuvaan 8 on piirretty optimaalinen (vihreä) virhekäyrä $\{(\sqrt{2(1-c)},\sqrt{2(1-\sqrt{1-c^2}}))\,|\, 0\leq c\leq 1\}$ ja sitä alhaalta rajaava suora $d_1+d_2=\sqrt 2$. Virhekäyrä ja sen yläpuolinen alue on suureiden $\sigma_1$ ja $\sigma_2$ mittausepätarkkuusalue $\mathsf{MUR}(\sigma_1,\sigma_2)$, epätarkkuusrelaationa $\Delta_2(\mathsf{M},\sigma_1)+\Delta_2(\mathsf{M}’,\sigma_2)\geq \sqrt 2$.
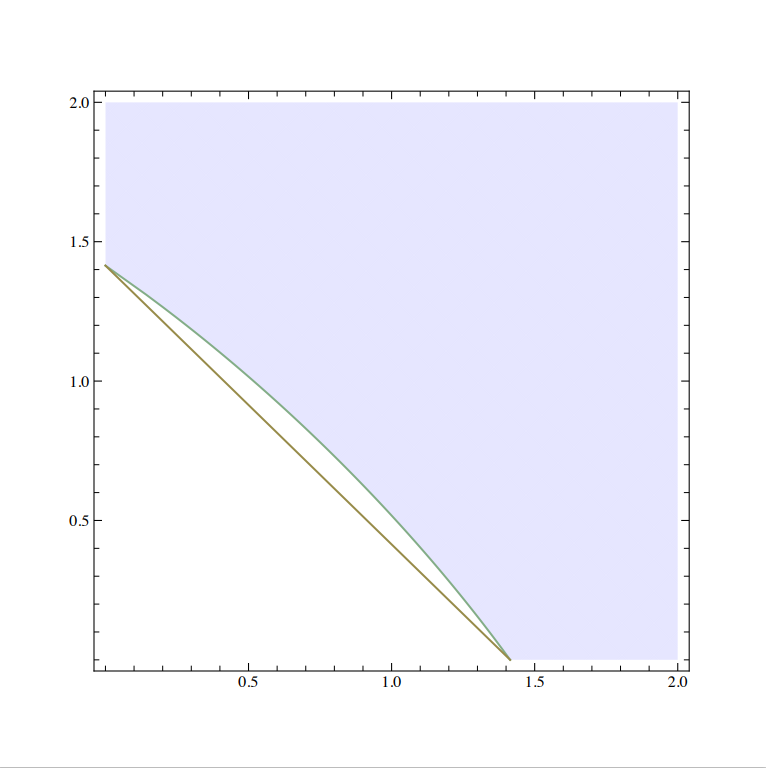
*****
Samoin eräiden keskeisten suureiden, kuten paikan $Q$ ja liikemäärän $P$, mittausepätarkkuusalue $\mathsf{MUR}(Q,P)$ ja sitä luonnehtivat epäyhtälöt, $Q$:n ja $P$:n mittausepätarkkuusrelaatiot tunnetaan. Tämän tapauksen matemaattinen käsittely edellyttää kuitenkin tekniikoita, joita ei voida tässä yhteydessä esitellä. Tulos on kuitenkin muotoiltavissa ilman tätä tekniikkaa. Olkoot $\mathsf{M}$ ja $\mathsf{M}’$ mitkä tahansa paikan $Q$ ja liikemäärän $P$ yhdessä mitattavissa olevat approksimaattorit. Jos molemmat kertaluvun 2 metriset virheet $\Delta_2(\mathsf{M},Q)$ ja $\Delta_2(\mathsf{M}’,P)$ ovat äärellisiä, niin on olemassa sellainen kaksoismittaus $\mathsf{G}$ ja sen määrittelevä tilaoperaattori $\rho$, mittauksen spesifioiva parametri, että
| (10.1) | $\Delta_2(\mathsf{M},Q)\Delta_2(\mathsf{M}’,P)\geq \Delta_2(\mathsf{G}_1,Q)\Delta_2(\mathsf{G}_2,P)\geq \Delta_\rho(Q)\Delta_\rho(P)\geq \frac{\hbar}2.$ |
Tässä $\mathsf{G}_1$ ja $\mathsf{G}_2$ kaksoismittauksen $\mathsf{G}$ määrittelemät marginaalisuureet. Alue $\mathsf{MUR}(Q,P)$ kattaa reunahyperbelinsä $d_1d_2=\frac{\hbar}2$ yläpuolisen alueen tason neljänneksessä $\mathbb{R}^+\times\mathbb{R}^+$. Kuvassa 9 on sen osa suorakaiteessa $[0,5]\times[0,5]$.
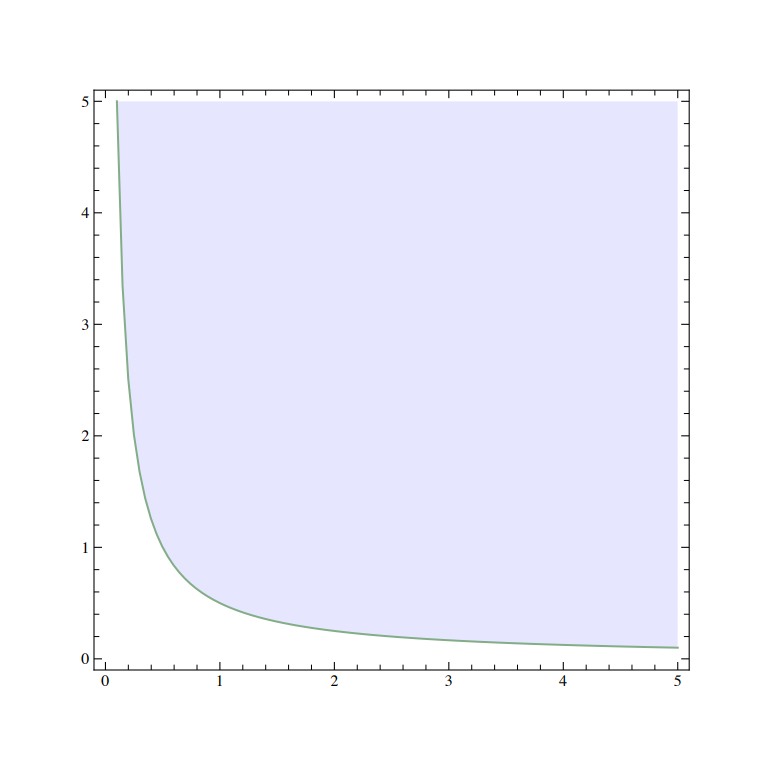
Lopuksi
Kvanttimekaniikan aito todennäköisyysluonne, puhtaiden tilojen superpositiot, tiettyjen suureparien yhteensopimattomuus, mittausten väistämättömät häiriöt sekä preparointeihin ja mittauksiin liittyvät epätarkkuusrelaatiot ovat kvanttimekaniikan keskeisiä klassisesta fysiikasta poikkeavia piirteitä. Tässä kirjoituksessa näitä teorian `outoja´ piirteitä on esitelty ns. kaksitasosyteemien teorian puitteissa, jossa tarvittava matematiikka on lähinnä algebrallista. Kirjoituksen alussa, Luku 2, kvanttimekaniikan `outoutta´on yritetty hälventää vertailemalla klassisen mekaniikan ja kvanttimekaniikan keskeisiä piirteitä yleisen probabilistisen teorian puitteissa. Fysikaalisen suureen matemaattisen esityksen yleistäminen teorian todennäköisyysteoreettista luonnetta paremmin vastaavaksi on paitsi laajentanut teorian puitteissa kuvattavissa olevia ilmiöitä, niin myös avannut mahdollisuuden mittausten aiheuttamien muutosten ja mittaustarkkuuksien johdonmukaiselle tarkastelulle. Tämä on mahdollistanut mm. Heisenbergin epätarkkuusrelaatioilleen antaman intuitiivisen mittaustarkkuuksia koskevan tulkinnan yksityiskohtaisen tutkimisen. Samalla kvanttimekaniikan peruskäsitteitä, tiloja ja fysikaalisia suureita, koskevat epätarkkuusrelaatiot ja alueet erottuvat toisistaan luonnollisella tavalla. Vaikka tässä kirjoituksessa asiaan ei suoranaisesti ole paneuduttu, katso kuitenkin yhtälö (10.1), todettakoon, että kaikissa tunnetuissa preparointeja ja mittauksia koskevissa tapauksissa mittausepätarkkuusrelaatiot voidaan palauttaa preparointiepätarkkuusrelaatioihin heijastaen sitä ilmeistä (jo Bohrin korostamaa) seikkaa että mittaamisen mahdollisuudet eivät voi ylittää preparoinnin mahdollisuuksia.
Yksi viime vuosisadan kuuluisimmista fyysikoista, Nobel-palkittu Richard Feynman (1918-1988), on myös suurelle yleisölle tuttu monista omaelämäkerrallisista tarinoistaan ja yleistajuisista kirjoistaan. [37] Feynmanilta on peräisi useita lentäviä lauseista, joista yksi on: ”I think it is safe to say that no one understands Quantum Mechanics”. [38] Tämä usein toistettu virke on, varsinkin näin valeuutisten aikakaudella, vahingollinen ja ehkä vaarallinenkin, sillä se luo asiayhteydestään irrotettuna sen kuvan, että teoria tunnettaisiin jotenkin heikosti. Tämä on tietysti epätosi. Kvanttimekaniikan matemaattinen ja käsitteellinen perusta tunnetaan erityisen hyvin ja sitä on tutkittu ehkä yksityiskohtaisemmin kuin mitään muuta fysiikan teoriaa. Feynman oli luonnollisesti hyvin tietoinen tästä asiantilasta. Tämän heiton voidaankin ymmärtää viittaavan siihen, että klassisesta fysiikasta tuttu, arkikokemukseen helposti liitettävissä oleva käsitteistö ei sovellu kvanttifysikaalisten ilmiöiden kuvaamiseen. Kvanttimekaniikka tunnetaan läpikotaisesti mutta ymmärrys voi joutua koetukselle kun pyrimme vastaamaan siihen keskeiseen maailmaa koskevaan kysymykseen: ”How the world could possibly be the way [Quantum Mechanics] says it is?”. [39] En yritä tässä vastata tähän kysymykseen, vaan tyydyn päättämään kirjoitukseni Eugen Wignerin (1902-1995) matematiikan roolia fysiikan teorioissa käsittelevän artikkelin ”The Unreasonable Effectiveness of Mathematics in the Natural Sciences” loppuhuomioon: [40]
The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve. We should be grateful for it and hope that it will remain valid in future research and that it will extend, for better or for worse, to our pleasure, even though perhaps also to our bafflement, to wide branches of learning.
*****
Kirjoitukseni on monin tavoin hyötynyt kolleegojeni professori emeritus Kari Ylisen ja dosentti Juha-Pekka Pellonpään kanssa käymistäni keskusteluista. Olen myös kiitollinen Dr. Tom Bullockille kuvien piirtämiseen saamastani avusta. Haluan lisäksi kiittää FM Hannu Korhosta ehdotuksesta ja kannustuksesta kirjoittaa kvanttimekaniikan peruskysymyksistä Dimensio-lehteen. Kiitos FM Riitta Salmenoja sujuvasta taittotyöstä.
*****
[1] Tällaisin odotuksin Euroopan komission teknologia-asioista vastaavan osaston varajohtaja Khalil Rouhana oli European Quantum Week -tapahtuman avauspuheenvuorossaan, 2.11.2020. Myös Suomessa ollaan asiassa liikkeellä: ”Mahdottoman mahdolliseksi tekevä laite” – Näin VTT:n johtaja kuvailee Suomeen tulevaa kvanttitietokonetta, Ylen tiedekirje 22.11.2020.
[2] Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen’, Zeithscrift für Physik 33 (1925) 879-893.
[3] Sitaatin alkuperä on epävarma, https://physicstoday.scitation.org/doi/10.1063/1.1768652, poimittu 31.10.2020, mutta olen kyllin vanha tunnistaakseni myös itse kyseisen asenteen kvanttimekaniikan opetusperinteessä.
[4] Tämä kaikki on hyvin dokumentoitu alan kirjallisuudessa, esimerkiksi teoksessa Quantum Measurement, P. Busch, P. Lahti, J.-P. Pellonpää, K. Ylinen, Springer, 2016, joka on myös tämän kirjoituksen taustalla.
[5] Joukon $\Omega$ osajoukkokokoelma $\mathcal{A}$ on $\sigma$-algebra jos se sisältää tyhjän joukon $\emptyset$ ja on suljettu komplementtiin ja numeroituvaan unioniin nähden; eli, jos $X\in\mathcal{A}$, niin myös $X’=\Omega\setminus X\in\mathcal{A}$, ja jos $X_i\in\mathcal{A}, i=1,2,\cdots$, niin myös $\cup_i X_i\in\mathcal{A}$.
[6] Teorian tilastollinen täydellisyys ei merkitse sen loogista täydellisyyttä.
[7] Konveksi joukko voidaan aina tulkita reaalisen vektoriavaruuden konveksiksi osajoukoksi, joten kyseinen kirjoitustapa on tässä perusteltu.
[8] Hyvä yhteenveto tällaisista kokeista on esimerkiksi osoitteessa https://physicsworld.com/a/the-double-slit-experiment/, haettu 2.10.2020.
[9] Louis de Broglien (1892-1987) esittämän aineaaltohypoteesin mukaan liikemäärän $p=mv$ omaavaan hiukkaseen liitty aalto, jonka aallonpituus on $\lambda=h/mv$. Kvanttifysikaalisten kokeiden semiklassisissa analyyseissa, esimerkiksi juuri ns. interferenssi-ilmiöiden yhteydessä, tyydytään usein käyttämään aineaaltohypoteesia ja soveltamaan klassista aalto-oppia ilmiön selittämiseksi. Vaikka näin saatavat tulokset ovatkin hyvin lähellä kvanttimekaniikan vastaavia tuloksia, niin on huomattava, että tällainen analyysi ei ole kvanttimekaniikkaa.
[10] https://www.hitachi.com/rd/research/materials/quantum/doubleslit/index.html, poimittu 26.20.2020.
[11] https://www.youtube.com/watch?v=jvO0P5-SMxk, poimittu 26.10.2020.
[12] Voidaan antaa useita ekvivalentteja muotoiluja.
[13] Tässä on käytetty epämuodollista kieltä, eikä esimerkiksi sanaan ”ominaisuus” sisälly tulkinnallista kannanottoa.
[14] Ääretönulotteista teoriaa tarvitaan esimerkiksi edellä kuvatun kaksoisrakokokeen kuvaamiseen tai esimerkiksi kvanttimekaniikan ehkä tärkeimmän yksittäisen tuloksen, aineen pysyvyyden todistukseen.
[15] Kaksiulotteinen vektoriavaruus on siinä mielessä `ahdas’ että se sisältää vain yksiulotteisia aitoja, nolla-avaruudesta poikkeavia, aliavaruuksia. Tämä seikka trivialisoi eräitä teorian piirteitä, jotka eivät kuitenkaan tässä ole erityisen merkittäviä.
[16] Tämä saadaan vaakavektorin $(\overline z,\overline w)$ ja pystyvektorin $\left(\begin{matrix} z\\ w \end{matrix}\right)$ Kroneckerin tulona.
[17] Kahden puhtaan tilan mahdolliset superpositiot on helpoimmin lausuttavissa niitä edustavien yksikkövektoreiden $(z,w),(u,v)$ normitettuna lineaarikombinaatioina $c(z,w)+d(u,v)=(cz+du,cw+dv)$, $c,d\in\mathbb{C}.$ Kun nämä vektorit ovat keskenään kohtisuorat ja $|c|=|d|=\frac 1{\sqrt 2}$, sanomme, että superpositio on tasapainoinen. Ks. myös Esimerkki 5.
[18] Tulos on oleellisesti peräisin jo von Neumannilta (1927) ja pätee yhtä hyvin ääretönulotteisessa teoriassa.
[19] Tässä ilmenee eräs kaksiulotteisen Hilbertin avaruuden erikoisuus: kaikki epätriviaalit ($\ne 0,I$) projektiot ovat yksiulotteisia, kuten puhtaat tilat. Yleisesti, puhdas tila on yksiulotteinen projektio, mutta projektio ei välttämättä ole yksiulotteinen.
[20] Tässä on oletettu että $b<a$, siis että $\boldsymbol{a}/{\left\|\boldsymbol{a}\right\|}=\boldsymbol{e}$.
[21] Jos $A=aE+b(I-E)$, $E$ efekti, niin $A^2=a^2E+b^2(I-E)$ jos ja vain jos $E^2=E$, siis kun $E$ on projektio (ja kyseessä siis $A$:n spektraalihajotelma).
[22]Jos $\boldsymbol{a}$ tai $\boldsymbol{b}$ on nollavektori, niin kyseinen suure on vakio ja siis triviaalisti $AB=BA$.
[23] Tässä näkyy taas 2-ulotteisen tapauksen erityisyys. Kun avaruuden dimensio kasvaa niin itseadjungoitujen operaattoreiden kommutatiivisuudelle tulee lisää tilaa.
[24] Tässä tapauksessa puhdas tila $\rho_{\boldsymbol{n}}$ on myös lausuttavissa puhtaiden tilojen $\rho_{\pm\hat{\boldsymbol{a}}}$ tasavahvana superpositiona, vrt. Esimerkki 5.
[25] Toisin kuin todennäköisyydet, keskiarvo ja varianssi riippuvat myös suureen arvojoukosta ja ovat siis laadullisia lukuja, vastaten suureen laatua.
[26] Yhtäpitävästi, jokainen $(z,w)\in\mathbb{C}^2$ voidaan lausua spinsuureen $\sigma_1$ ominaisvektoreiden $\frac 1{\sqrt 2}(1,1)$ ja $\frac 1{\sqrt 2}(1,-1)$ lineaarikombinaatioina muodossa $(z,w)=\frac 12(z+w)(1,1)+\frac 12(z-w)(1,-1)$. Se, että jokainen puhdas tila $\rho_{\hat{\boldsymbol{n}}}$ voidaan lausua minkä tahansa kahden muun puhtaan tilan $\rho_{\pm\hat{\boldsymbol{a}}}$ superpositiona, on taas eräs kaksiulotteisen Hilbertin avaruuden erikoisuus.
[27] Huomaa, että toiset yhtäsuuruudet seuraavat $\mathsf{G}$:n mittaominaisuudesta ja siitä että kaksiot, esimerkiksi $\{a,b\}$, ovat erillisten yksiöiden $\{a\}$ ja $\{b\}$ unioneja.
[28] Huomaa, että jos $\boldsymbol{e}\parallel\boldsymbol{f}$, niin ehto toteutuu aina.
[29] Tämä tarkoittaa sitä, että $\gamma(X,\Xi)=p(X), \gamma(\Omega,Y)=q(Y)$, $X\in\mathcal{A}\subset 2^\Omega, Y\in\mathcal{B}\subset 2^\Xi$.
[30] Jälkimmäinen yhtäsuuruus tarkoittaa sitä, että infimum, suurin alaraja, saavutetaan eli on minimi.
[31] Tämä alue riippuu luonnollisesti käytetystä `leveysmitasta’, joka tässä on valittu hajonnaksi.
[32] Diracin vakio $\hbar$, Planckin vakio jaettuna $2\pi$:llä, on tässä laatusyistä, $[{\rm paikka}]\times[{\text{ liikemäärä}}]=\mathrm{kgm^2/s} = \mathrm{Js} = [h]$.
[33] Ks. esm. Quantum Measuremen, ibid., Luku 15.3.
[34] Oletamme taas, että suureet $\mathsf{M}$ ja $\mathsf{M}’$ ovat myös $\pm 1$-arvoisia.
[35] Joukko riippu käytetyistä virhemitoista.
[36] Kuvattu yksityiskohtaisesti mm. teoksessa Quantum Measurement, ibid., ss 333-338.
[37] R. P. Feynman, ”Surely You’re joking, Mr. Feynman!”, 1985, ”What Do You Care What Other People Think?”, 1988. ”The Character of Physical Law”, 1965, ”QED, The Strange Theory of Light and Matter”, 1985.
[38] https://www.spaceandmotion.com/quantum-mechanics-richard-feynman-quotes.htm, poimittu 16.11.2020.
[39] Bas van Fraassen, Quantum Mechanics: an empiricist view, Clarendon Press, 1991.
[40] http://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html, poimittu 19.11.2020.
Liite: Äärellisulotteinen Hilbertin avaruus
Hilbertin avaruus $H$ on esimerkki vektoriavaruudesta, ja tässä esityksessä sen skalaarikunta on kompleksilukujen joukko $\mathbb{C}$. Tämä merkitsee että on määritelty $H$:n alkioiden (eli vektoreiden) yhteenlasku $(u,v)\mapsto u+v$ ja skalaarilla kertominen $(\lambda,u)\mapsto \lambda u$, jotka täyttävät muutaman luonnollisen ehdon. Vektoriavaruuden rakenteen lisäksi Hilbertin avaruudessa on määritelty tietyt ehdot täyttävä kompleksilukuarvoinen skalaari- eli sisätulo, $(u,v)\mapsto\langle u|v\rangle$. Se on lineaarinen jälkimmäisen argumentin suhteen ja $\langle u|v\rangle=\overline{\langle v|u\rangle}$ (kompleksikonjugaatti). Lisäksi $\langle u,u\rangle\geq0$ kaikilla $u$, ja $\langle u|u\rangle=0$ vain jos $u=0$. Sisätulon avulla määritellään vektorin $u\in H$ normi eli pituus $\left\|u\right\|=\sqrt{\left\langle u | u \right\rangle}$. Hilbertin avaruuden määritelmään kuuluu vielä ns. täydellisyys normin suhteen, muttä tämän käsittelyn sivuutamme. Se on ilman eri oletusta voimassa äärellisulotteisessa tilanteessa, jota tässä kirjoituksessa lähinnä käsittelemme. Äärellisulotteisuus merkitsee, että $H$:ssa on äärellinen kanta eli sellainen joukko $\{u_1,\dots, u_n\}\subset H$, että jokainen $u\in H$ voidaan esittää yksikäsitteisellä tavalla muodossa $u=\sum_1^n\lambda_iu_i$, missä $\lambda_i\in \mathbb{C}$. Tässä tilanteessa $n$ on yksikäsitteisesti määrätty, ja sitä sanotaan $H$:n dimensioksi. Kantavektorit $u_i$ voidaan valita keskenään kohtisuoriksi eli ortogonaalisiksi: $\left\langle {u_i} | {u_j} \right\rangle=0,i\ne j$, ja yksikkövektoreiksi, $\left\|{u_i}\right\|=1$. Tällöin $\lambda_i=\left\langle u_i | u \right\rangle$. Oletamme jatkossa, että kanta on näin valittu (eli kanta on ortonormaali). Kun kanta $\{u_1,\dots, u_n\}\subset H$ on kiinnitetty, voidaan vektori $u\in H$ samaistaa skalaarikunnan $\mathbb{C}$ n-kertaisen karteesisen tulojoukon $\mathbb{C}^n$ alkioon $(\lambda_1,\ldots,\lambda_n)$. Valitut kantavektorit $u_1,\ldots,u_n$ näyttäytyvät tällöin $\mathbb{C}^n$:n vektoreina $(1,0,\cdots),\ldots, (0,\cdots,1)$.
Äärellisulotteisessa tapauksessa kvanttimekaniikan kannalta keskeinen Hilbertin avaruuden $H$ operaattoriteoria palautuu lineaaristen kuvausten, operaattoreiden $A:H\to H$ teoriaan. Kuvaus $A:H\to H$ on lineaarinen jos sen on additiivinen, $A(u+v)=Au+Av$, ja homogeeninen, $A(\lambda u)=\lambda Au$, kaikilla $u,v\in H, \lambda\in\mathbb{C}$. Kun kanta $\{u_1,\dots, u_n\}\subset H$ on kiinnitetty, operaattori $A:H\to H$ määräytyy sisätulon ominaisuuksien nojalla täysin kompleksiluvuista $a_{ij}= \left\langle u_i | Au_j \right\rangle$, $i,j=1,…,n$. Ne muodostavat operaattorin $A$ matriisin $(a_{ij})$ kannan $\{u_1,\dots, u_n\}$ suhteen. Operaattorin $A$ kaikki ominaisuudet voidaan ilmaista myös sen matriisiesityksen avulla. Kun operaattorit esitetään matriiseina, niin vektorit, joihin operaattorit operoivat, kirjoitetaan komponenttimuodossaan yleensä pystyvektoreina. Tilasyistä emme juurikaan käytä tätä kirjoitustapaa.







