Konkreettisia kokemuksia algebran pohjaksi
Siirtyminen kuudennelta luokalta seitsemännelle merkitsee matematiikan opiskelussa suurta hyppäystä monella tavalla, matematiikassa erityisesti sen takia, että konkreettisesti miellettävään matematiikkaan tulee uusia abstrakteja aineksia. Muutoksen ei tarvitsisi olla jyrkkä, sillä algebraankin on olemassa konkreettista ajattelua tukevia opetusvälineitä.
Joskus aikanaan vuosia sitten olin kirjannut muistiin kokemuksiani seitsemännen luokan algebran opettamisesta. [1] [2]. Jo silloin olin yrittänyt suunnitella jotain konkreettista materiaalia, jonka avulla oppilaita olisi voinut tutustuttaa muuttujan lausekkeisiin ja harjoittaa niiden muodostamista jo ennen kuin siirryttäisiin varsinaisiin polynomilaskuihin.
Siksi olikin miellyttävä yllätys saada havaita, että vihdoinkin sellainen oppimisväline on olemassa. NCETM (National Centre for the Excellence in the Teaching of Mathematics) kertoi marraskuun 2019 tiedotuslehdessään [3] konkreettisista oppimisvälineistä (mathematical manipulatives and representations), joita käytetään Englannissa yleisesti 11–14-vuotiaiden opettamisessa (key stage 3). Yksi näistä on algebrakortit (algebra tiles).
Vastaava sähköinen tuote on vapaasti käytettävissä Hoodamat-verkkomateriaalissa. [4]. Sähköisyydestä on se etu, että x-kortin pituus ja samalla siis neliön sivu on säädettävissä. Muuttujavaikutelma on siten todellisempi, koska kortit ovat aidosti muuttuvia. Opetusohjeita tällä sivulla ei ole.
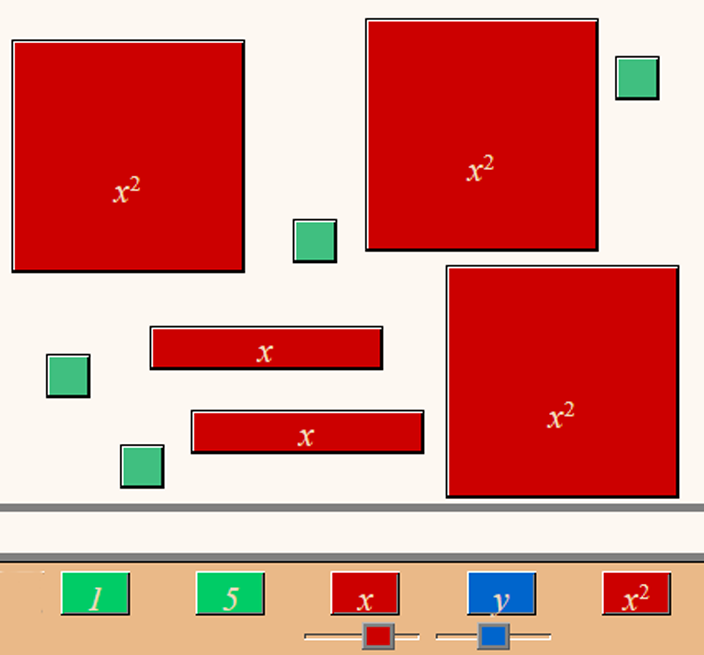
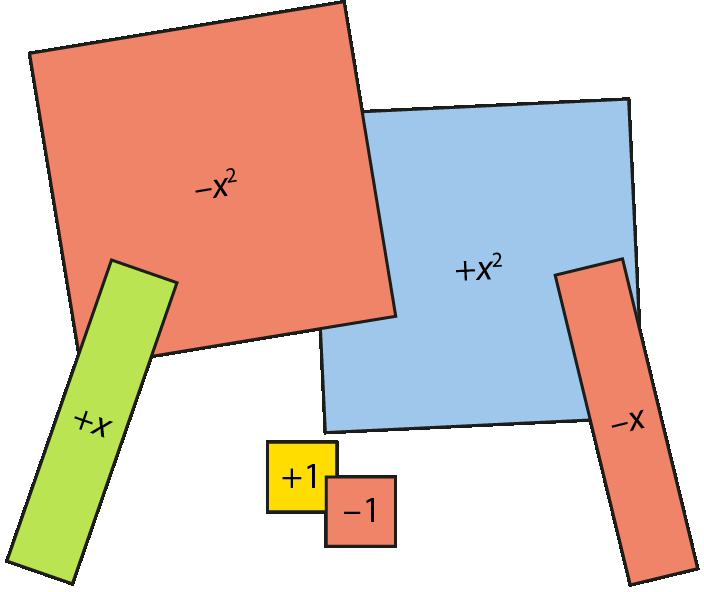
Hoodamathin algebrakortit keskittyvät lausekkeen muodostamiseen ja samanmuotoisten termien konkreettiseen yhdistämiseen, sillä negatiivisia kertoimia ei ole. Vastapainoksi siinä on kaksi muuttujaa. NCETM:n materiaali on kuitenkin tavallaan konkreettisempi, koska se koostuu käsin kosketeltavissa korteista. Sillä voidaan harjoitella myös kokonaislukujen yhteenlaskua, sillä korttiparit ”+1” ja ”−1”, ”+x” ja ”−x” sekä ”+x²” ja ”−x²” kumoavat toisensa ja poistuvat yhteenlaskusta. Siihen liittyy myös 20-sivuinen, pdf-muotoinen opettajanopas [5], todellinen kultakaivos opettajalle.
NCETM:n kortit ovat sillä tavalla avoimempi materiaali, että korttikokoelma on kohtuullisen vaivattomasti myös itse tehtävissä. Samalla sitä voitaisiin täydentää toisella tai useammallakin muuttujalla. Ja jos vain aika ja askarteluhalu myöten antavat, niin myös kolmannen asteen termeillä, jotka luonnollisesti olisivat kolmiulotteisia, siis suorakulmaisia särmiöitä.
Viitteet:
[1] Korhonen, H. Seiskan nivel laskennosta algebraan. Dimensio: 68 (2004): 1, s. 20–22.
[2] Korhonen, H. Xylitolihedelmiä ja zitroonia. Seiskaluokkalaiset algebraa oppimassa. Dimensio: 68 (2004): 3, s. 15–18.
[3] NCETM Newsletter – November 2019 osoitteessa https://www.ncetm.org.uk/news/54069.
[4] HoodaMath Algebra tiles osoitteessa http://www.hoodamath.com/mobile/games/algebratiles.html.
[5] MathHUBS Resources. Mastery Professional Development. Mathematical representations. Algebra tiles. Guidance Document. Keystage 3. Linkki.
Aloituskuva: BiZkettE1 / freepik.com