Jänne–kaari-tehtävän ratkaisuja GeoGebralla
Jari Sääksjärvi esitteli 31.7.2020 tässä lehdessä likiarvokaavan ympyrän säteen laskemiseksi segmentin kaaren ja jänteen pituuksien avulla. Se on sellaista matematiikkaa, jota minulle opetettiin aikanaan sekä koulussa että jatko-opinnoissa ja varmaankin Jarpille insinööriopinnoissa. Tällaiset laskut kuuluvat kuitenkin menneeseen maailmaan ainakin koulun kannalta katsottuna, sillä matematiikkaohjelmat avaavat ihan uusia mahdollisuuksia. Esimerkiksi GeoGebra tarjoaa useampia ratkaisutapoja.
Ratkaisu suoraan konstruktiopiirroksesta
Ongelman geometria on hyvin yksinkertainen. Piirretään pisteet A, B ja C sekä jana AC ja kaari ABC. Kaaren päätepisteisiin piirretyt kaaren normaalit määrittävät kaariympyrän keskipisteen O. Kysytty säteen pituus on keskipisteen ja kaaren päätepisteen välimatka, jonka GeoGebra näyttää pyydettäessä (kuva 1).
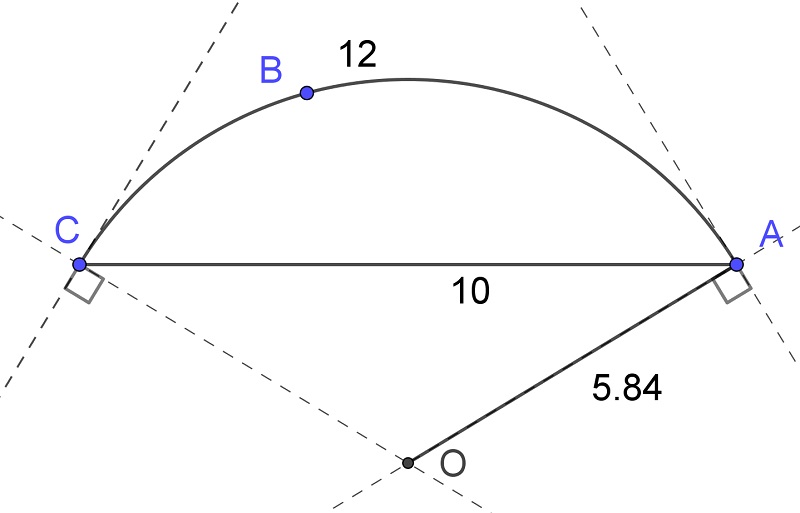
Piirrosratkaisun lähtöarvojen antamisessa on se vaikeus, että GeoGebrassa ei ole valmista työvälinettä annetun pituisen kaaren piirtämiseen. Annettuihin pituuksiin, tässä jänne = 10 ja kaari = 12, päästään raahaamalla ensin jänteen päätepistettä ja sitten kaaren määrittävää pistettä B. Tarkempaa tulosta haluttaessa voidaan suurentaa kuvaa hiiren vierityspainikkeella, jolloin raahaaminen on tarkempaa, ja palata sitten takaisin standardinäkymään.
Ratkaisu kahden lukumuuttujan avulla
Jarpin likiarvokaavaa tarkempiin likiarvotuloksiin päästään kuitenkin kohtuullisen helposti seuraavalla kaksivaiheisella menettelyllä. Olkoot annettuina jänteen pituus 5 ja kaaren pituus 10. Asetetaan jänne (jana) annetun pituiseksi liu’un (graafisen lukumuuttujan) avulla. Säädetään kaaren pituus likimäärin oikeaksi toisella liu’ulla, joka siirtää kaariympyrän keskipistettä janan keskinormaalilla (kuva 2).
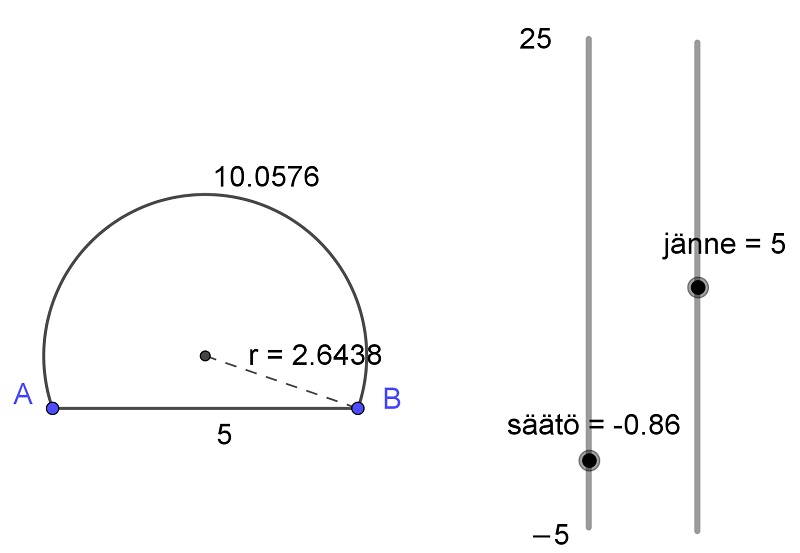
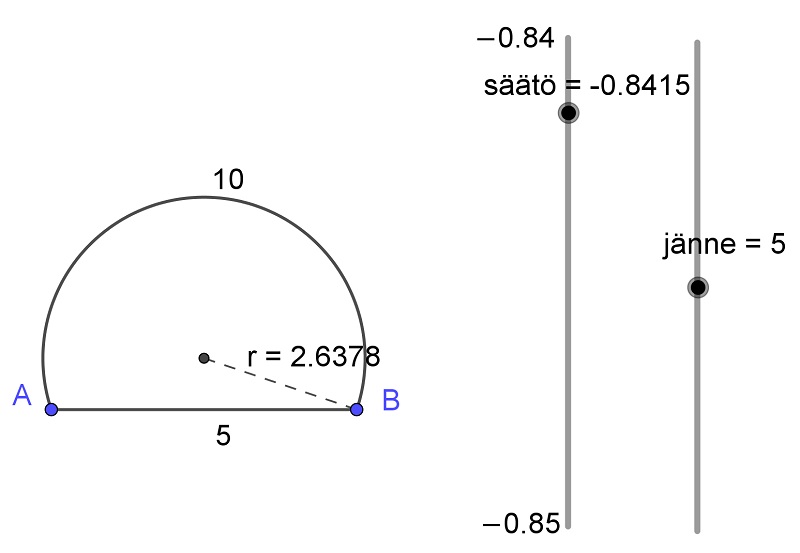
Muutetaan säätöliu’un rajoja lähemmäs tarvittavaa arvoa, jotta saadaan liu’un askellus tarkemmaksi. Neljän desimaalin tarkkuudella säde on 2,6378, kun jänne on 5,0000 ja kaari on 10,0000 (kuva 3). (GeoGebrahan ei näytä desimaaliosaa, jos desimaalit ovat kaikki nollia halutulla tarkkuudella!)
Ratkaisun kelvollisuus?
Mielenkiintoista olisi tietää, hyväksyisivätkö lukion opettajat tai jopa ylioppilastutkintolautakunta tällaisen likiarvoratkaisun täysin pistein, jos mukana olisivat kuvat 2 ja 3 sekä seuraava selitys metodista:
Piirretään GeoGebran vakiotyövälineellä jana AB, jonka pituutta voidaan säätää liu’ulla (nimeltä ”jänne”). Merkitään sen keskinormaalille piste O, jonka paikkaa voidaan säätää toisella liu’ulla (nimeltä ”säätö”). Piirretään GeoGebran vakiotyövälineellä ympyränkaari keskipisteenä O ja päätepisteinä A ja B. Etsitään O:lle paikka, joka antaa kaarenpituudelle arvon likimäärin 10. Vaihdetaan liu’un vaihteluväliä niin lähelle tätä arvoa, että saadaan kaaren pituudeksi 10 ilman desimaaleja halutulla tarkkuudella.
Jotta ratkaisu ei tulisi hylätyksi sitä tarkemmin miettimättä, niin kannattaa huomata, että menetelmä on sikäli yleinen, että sekä janan että kaaren pituutta voidaan säätää vapaasti toisistaan riippumatta (kaaren pituus luonnollisesti aina suurempi kuin janan). Lisäksi lukujen näyttämisen tarkkuutta eli desimaalien määrää voidaan säätää GeoGebran asetuksista.
Yllättäen tarkkuudessa ei tulekaan ensin vastaan GeoGebran laskentatarkkuus (viisitoista desimaalia), vaan paljon aikaisemmin liu’un askellus. Pienin hyväksyttävä askellus, jota GeoGebra ei pyöristä tasan nollaksi, on sadasmiljoonasosa (kahdeksan desimaalia). Niinpä esimerkiksi kahdeksan merkitsevän desimaalin tarkkuudella GeoGebra antaa säteen pituudeksi 2,63783441, kun janan pituus on 5 (tasan) ja kaaren 10,00000000.
CAS-ratkaisu
Jos vain numeerinen tulos kiinnostaa, niin Jarpin ongelmaan on paljon helpompikin ratkaisu. Valitse Geogebran asetuksista pyöristystarkkuudeksi 15 desimaalia ja kirjoita CAS-ikkunaan komento
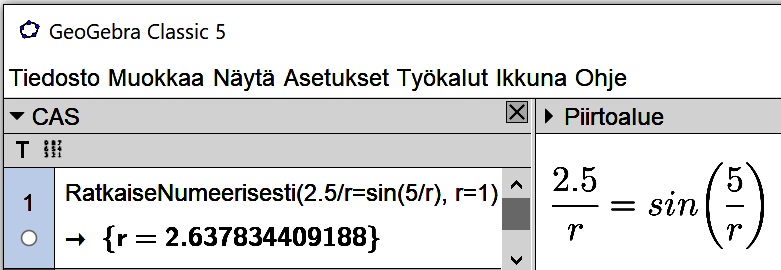
RatkaiseNumeerisesti(2.5/r=sin(5/r), r=1)
missä 2.5 on jänteen ja 5 kaaren puolikas, r komennon sisäinen parametrimuuttuja sekä r = 1 iteroinnin alkuarvo. Tulos on r = 2,637834409188. Ratkaistavan yhtälön saat helposti, kun piirrät kuvioon kaarenpuolikasta vastaavan keskuskulman, kirjoitat kaksi yksinkertaista yhtälöä ja eliminoit niistä kulman.