Fibonaccin sanoja
Fibonaccin sanoiksi sanotaan kahdesta merkistä rekursiivisesti rakentuvia merkkijonoja. Käytämme esimerkkinä jonoa 0, 1, 10, 101, 10110, 10110101, 1011010110110, … Jos sen tutkiminen ei kovin hyödyllistä olekaan, niin metkaa se voi olla (metka matematiikka = recreational mathematics). Samalla voi oppia ongelmanratkaisua ja uusia asioita käyttämästään matematiikkatyövälineestä.
Fibonaccin sanoista on kirjoitettu paljon [1]. Merkkijonot voidaan rakentaa yhtä hyvin myös kahdesta kirjaimesta tai muistakin merkeistä. Tämä jono esiintyy lukujonojen verkkolistassa OEIS numeroilla A036299 ja A061107. Muitakin määrittelyjä on [2]. Ne eroavat useimmiten toisen jäsenen osalta. Tämän jonon olemme valinneet siksi, että nämä sanat voidaan tulkita myös binaariluvuiksi.
Verkossa on myös erityistyöväline Fibonaccin sanojen tuottamiseen [3]. On kuitenkin ihan eri asia osata tehdä itse kuin käyttää valmista. Saat valita merkkisi itse ja muokata tuottamissääntöä halusi mukaan sekä tuottaa niin monta sanaa kuin haluat.
Tutkitaan Fibonaccin sanojen tuottamista GeoGebran taulukkolaskennassa. Varataan laskentataulukon ensimmäinen rivi otsikoille (kuva 1). Kirjoita soluun A2 luku 0 ja soluun A3 luku 1. Valitse alue A2:A3 ja monista alaspäin kahvan avulla. Näin saadaan jonojen termeille indeksi.
Luodaan Fibonaccin sanat vastaavalla tavalla B-sarakkeeseen. Kirjoita soluun B2 teksti ”0”, soluun B3 teksti ”1” ja soluun B4 kaava B3+B2 (tämä ilman lainausmerkkejä; GeoGebran kaavaa ei tarvitse aloittaa yhtäsuuruusmerkillä niin kuin Excelissä). Kun valitset solun B4 ja monistat kahvan avulla alaspäin, niin huomaat tutun lukujonon. Periaate on samanlainen kuin Fibonaccin lukuja muodostettaessa. Nyt vain lukuja ei lasketa yhteen, vaan kaksi viimeistä kirjoitetaan peräkkäin merkkijonoina; viimeinen ensin ja sen jälkeen viimeistä edellinen.
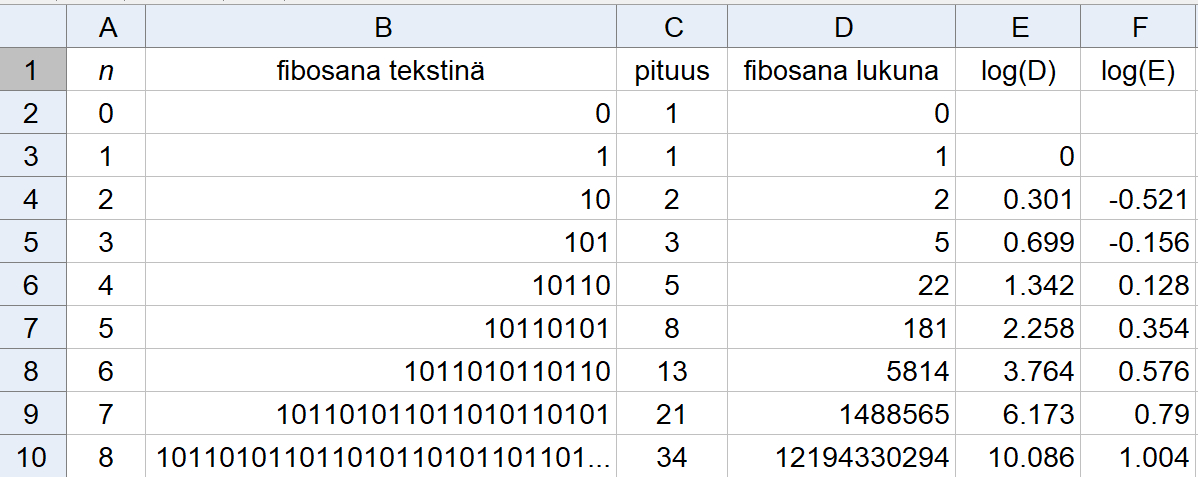
Fibonaccin sanojen pituus saadaan kirjoittamalla soluun C2 kaava Pituus(B2) (taas ilman lainausmerkkejä) ja monistamalla alaspäin. Muunnetaan vielä fibosanat luvuiksi. Kirjoita soluun D2 kaava MuunnaKymmenjärjestelmään(B2, 2) ja monista alaspäin kahvan avulla. Komennon toinen parametri kertoo, mitä pidetään muunnettavan luvun kantalukuna. Luvut kasvavat aika vikkelästi. Kuudestoista fibosana kymmenjärjestelmässä on 9.28418577192773*10^296 ja seuraava on jo GeoGebralle liian suuri.
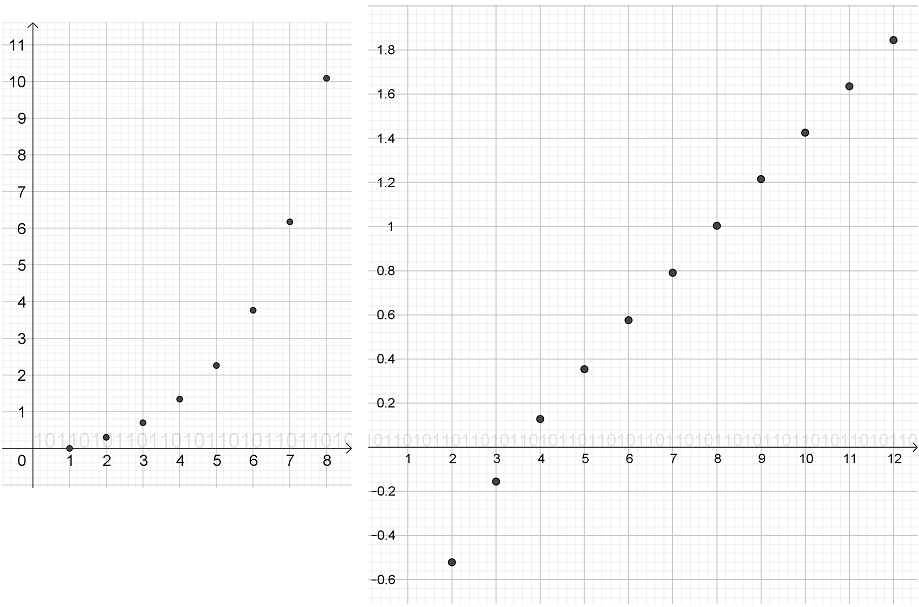
Tutkitaan vielä kasvunopeutta. Kirjoita soluun E3 kaava lg(D3) ja monista alaspäin. Piirretään jonon logaritmin arvot järjestysluvun funktiona (kuva 2a). Valitse alue A3:A15 ja ctrl-näppäin (Macissa cmd) pohjassa alue E3:E13 ja klikkaa Luo pistelista -työkalua. Fibosanojen logaritmitkin näyttävät kasvavan jotakuinkin eksponentiaalisesti, joten kasvu on nopeampaa kuin eksponentiaalinen.
Piirretään vielä logaritmien logaritmit (kuva 2b). Kasvu on nyt lineaarista. Siis luvuiksi tulkittujen fibosanojen logaritmit kasvavat eksponentiaalisesti eli kasvu on tavallaan kahteen kertaan eksponentiaalista eli muotoa $a^{a^x}$. Tämän tyyppisiä funktioita kutsutaan englanniksi nimellä double exponential function [4].
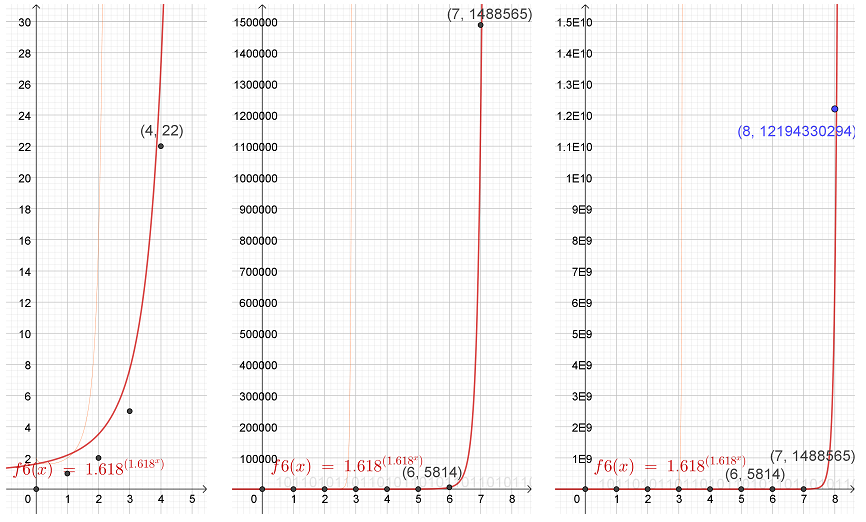
Tutkimalla lukujonon logaritmin logaritmin kulmakerrointa herää epäily, että fibosanojen tapauksessa kyseinen a saattaa olla lähellä kultaisen leikkauksen lukua φ ≈ 1,618 suurilla x:n arvoilla. Epäily vahvistuu hypoteesiksi jo muutamasta piirroksesta, sillä jo seitsemäs piste on käyrällä kuvan tarkkuudella (kuva 3). Kuvan avulla tutkiminen ei ole kovin havainnollista, sillä luvuiksi tulkitut fibosanat kasvavat niin nopeasti, että viimeistä edelliset pisteet näyttävät olevan aina lukumääräakselilla.
Fibonaccin sanojen tuottaminen ja tutkiminen onnistuvat tietysti muillakin matematiikkavälineillä, sillä niissä on yleensä riittävästi merkkijonojen käsittelykomentoja. Kaikilla vain on oma lauseoppinsa, joka on opeteltava jokaisen ohjelman kohdalla erikseen. Esimerkiksi Excelissä merkkijonojen yhdistämismerkki on ”&”, ilman lainausmerkkejä, ja kaavan alkuun pitää kirjoittaa yhtäsuuruusmerkki ”=”. Ohjelmoimallakin Fibonaccin sanoja voidaan tuottaa helposti, esimerkiksi Logolla tai Pythonilla, mutta tutkiminen tuntuu käyvän sujuvimmin GeoGebralla. Monipuolisista työvälineistä Mathematica olisi GeoGebraa ammattimaisempi ja tehokkaampi, mutta sitä ei taida olla kouluissa kovin yleisesti.
[1] Katso esimerkiksi Chuan, W. Generating Fibonacci words osoitteessa
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.376.63&rep=rep1&type=pdf
[2] Esimerkiksi Fibonacci word osoitteessa https://en.wikipedia.org/wiki/Fibonacci_word
[3] Fibonacci word generator osoitteessa https://onlinemathtools.com/generate-fibonacci-words
[4] Double exponential function Wikipediassa: https://en.wikipedia.org/wiki/Double_exponential_function







