Askartelua ja aivojumppaa: pop up 1
Ponnahduskortti (pop up -kortti) on taittokortti, josta ponnahtaa esiin kolmiulotteinen rakennelma, kun kortti avataan. Samalla periaatteella on tehty myös kirjoja, joiden jokainen aukeama toimii ponnahduskortin tapaan. Niiden hahmottaminen ja varsinkin suunnittelu sisältävät paljon matematiikkaa, joka ei aina edes näytä matematiikalta, vaan hauskalta askartelulta. Pop up -korttien rakenteen matematiikasta on saatu uusi merkittävä tulos ihan vastikään.
Verkossa on pilvin pimein ohjeita pop up -korttien tekemiseen. Google haku ”pop up cards” antaa lähes neljä miljoonaa osumaa, vastaava haku ranskaksi runsaat kaksisataatuhatta ja suomeksikin toistakymmentä tuhatta. Ohjeet ovat monesti niin perusteelliset ja yksityiskohtaiset, että kortin geometriaa ei tarvitse pohtia, esimerkiksi kukkakortti [1]. Tarjolla on myös ideoita, joiden geometrian joutuu itse miettimään [2].
Alalla on myös laaja kaupallinen tuotanto. On lastenkirjoja, oppimateriaalia ja kortteihin erikoistuneita yrityksiä. Lopputuotteet saattavat olla hyvin monimutkaisia vai mitä sanot Helsingin tuomiokirkosta. Kortti on suunniteltu ja valmistettu pienessä pop up -kortteihin erikoistuneessa perheyrityksessä Vietnamissa. Suomessa kortteja markkinoi PopUp 3D Card Finland [3].

Pop up -kortti on aina taittokortti. Sisältö paljastuu vasta korttia avattaessa. Kortti sisältää siten jo sinänsä rakenteellisen yllätyksen. Yksinkertaisimmat matemaattiset pop up -kortit saadaan paperi- tai kartonkiarkista. Arkki taitetaan ja siihen tehdään tarvittavat leikkaukset. Taitellaan sopivasti. Suljetaan ja avataan. Matemaattisena esimerkkinä on itse ehty pop up -kortti, jonka tekemiseen tarvitaan vain suoria leikkauksia. Kuvasta on helppo nähdä, että kyseessä on fraktalisoituva rakenne, vaikka leikkaaminen ja taivuttelu ei onnistukaan kovin pitkälle käytännössä.

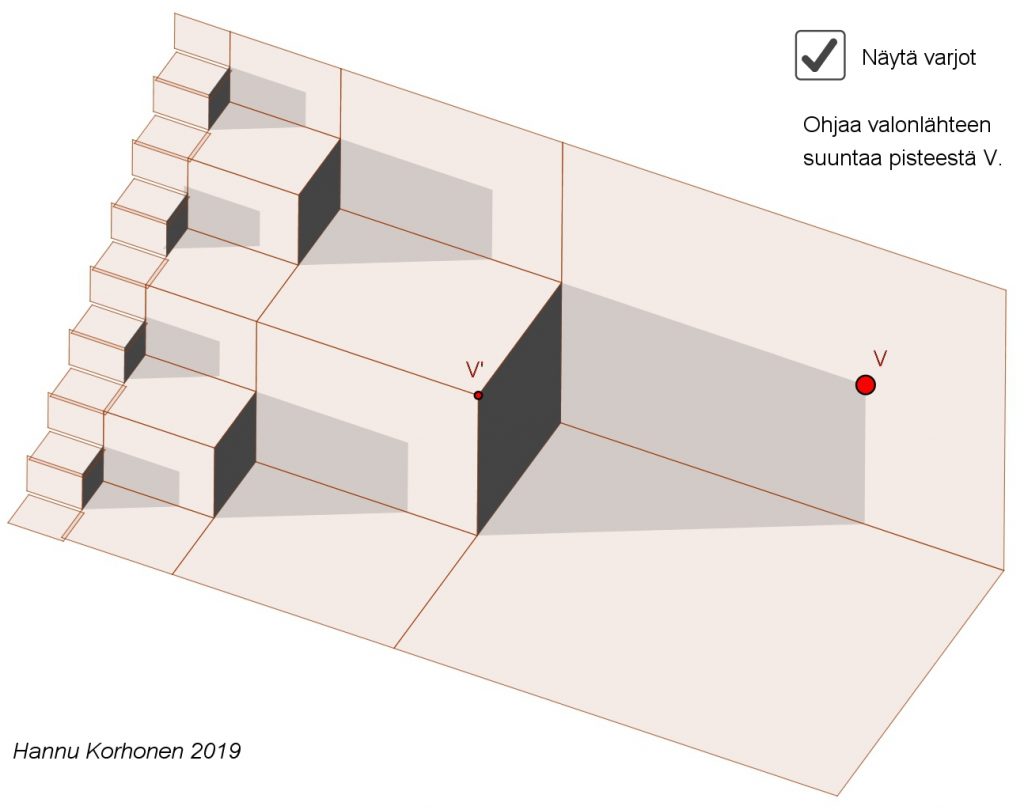
Kortin matematisointia voi jatkaa esimerkiksi laatimalla siitä sähköinen malli jollakin piirto- tai matematiikkaohjelmalla. Itse käytin GeoGebraa. Tällaisessa harjoituksessa on kyse ehkä enemmänkin matematiikan tekemisestä ja matemaattisen ajattelun ja hahmottamisen oppimisesta kuin tietyn matemaattisen sisällön tai käsitteen oppimisesta. Lisähaastetta saa esimerkiksi siitä, että dynaamiseen kuvaan mallinnetaan myös rakenneosien heittämät varjot [4].
Runsaampia värejä ja muotoja saadaan liimaamalla tai muuten liittämällä esiin ponnahtaviin osiin erikseen leikattuja kuvioita. Ensimmäisessä kuvassa oleva Helsingin tuomiokirkko on tuotettu juuri tällaisella tekniikalla. Pelkästään leikkauksien avulla tehtyjen pop up ‑korttien mahdollisuudet ovat paljon suuremmat kuin niiden käyttäminen lasten askartelussa.
Vastikään on nimittäin osoitettu, että valitsemalla leikkaukset sopivasti on mahdollista tuottaa paperiarkista tai muusta materiaalilevystä mikä tahansa ennalta määrätty muoto [5]. Tulos vastaa taiteilijan mielikuvituksen vaatimuksia, matemaatikon ajattelun tarkkuutta (rigour) ja insinöörin konstruktiivista ajattelua, sanovat tutkijat. Näin paperin leikkelyn taiteesta on tullut myös matematiikan ja tekniikan osa-alue. Itse asiassa ei ole aina ihan helppoa sanoa, ovatko tuotokset taidetta, matematiikkaa vai teknologiaa [6], [7], [8].
Lisää luettavaa
[1] Helppo kukkiva pop-up-kortti. Kodin kuvalehti 13.5.2017 osoitteessa https://www.kodinkuvalehti.fi/blogit/arjen-varipilkut, viitattu 11.1.2020.
[2] Anun askareet. Pop up -kortti lapselle osoitteessa https://anunaskareet.blogspot.com/2017/09/pop-up-kortti-lapselle.html, viitattu 11.1.2020.
[3] PopUp 3D Card Finland osoitteessa https://www.facebook.com/pg/popupcardfinland/about/?ref=page_internal
[4] Pahvintaittelu. Geogebra-materiaali osoitteessa https://www.geogebra.org/m/buxmcvvf.
[5] Mathematical framework turns any sheet of material into any shape using kirigami cuts. Science Daily 20.8.2019, https://www.sciencedaily.com/releases/2019/08/190820164634.htm, viitattu 11.1.2020.
[6] Kirigami paper art pop-up card easy osoitteessa https://www.youtube.com/watch?v=6C5AbMSrmPY, viitattu 11.1.2020.
[7] Como fazer kirigami anéis quadrados versão osoitteessa https://www.youtube.com/watch?v=4WVLg1tUiKs, viitattu 11.1.2020.
[8] Fretwork (scrollsaw) bowl. Cutting process and final result osoitteessa https://www.youtube.com/watch?v=4WVLg1tUiKs, viitattu 11.1.2020.







