Askartelua ja aivojumppaa: mekaaniset pulmat 2
Valtaosa mekaanisista pulmista on vain erikoisharrastajien kohteita eivätkä ne sovellu koulun arkityöhön erikoisuutensa takia, esimerkiksi pulmalukot, tai vaikeutensa ja monimutkaisuutensa takia, esimerkiksi pirunnyrkit. Koottavissa pulmissa on kuitenkin monia, jotka sopivat innostuksen herättämiseen, ajattelun virittämiseen ja ongelmaratkaisun opettamisen millä koulutustasolla tahansa. Monet niistä ovat rakenteeltaan niin yksinkertaisia, että pulmaesineitä voi valmistaa itsekin. Toimintatapoja on siten useita: valmiin pulman ratkaiseminen, pulmaesineen valmistaminen tai aivan uuden pulman määrittely tai keksiminen.
Mekaanisten pulmien ja konkreettisten oppimisvälineiden raja ei ole jyrkkä, vaikka syntyfilosofia on erilainen. Esimerkiksi tangramia pidetään mekaanisena pulmana, vaikka se on oikeastaan vain palapeli eikä väline sinänsä muodosta mitään tiettyä ratkaistavaa pulmaa. Opetuksen kannalta hyvin samankaltaisia ongelmia voidaan muotoilla geometristen ja loogisten palojen sekä rakentelulevyjen ja ‑kuutioiden avulla. Pulmaesineiden tekeminen itse aktivoi ratkaisijaa, syventää ongelmanratkaisun kokemusta ja liittää matemaattiseen ongelmaan sellaisia kokemuksia, joita kirjallinen tehtävä tai valmis materiaali ei anna.
Tasavartinen risti ja muut vastaavat geometriset palapelit olivat hyvin suosittuja edellisen vuosisadan alkupuolella myös ajanvietetehtävinä. Siitä on monta muunnelmaa. Monista niistä voitiin koota ristin lisäksi muitakin kuvioita [1]. Uusia ongelmia saadaan jakamalla tavoitekuvio eri tavoin. Palapelin materiaaliksi kelpaa paperi tai kartonki.
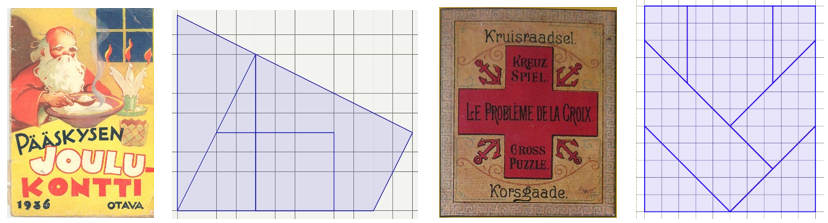
T-pulma todistaa, että muutamankin palan palapelin kokoaminen saattaa olla hankalaa, vaikka tavoiteltu muoto olisi tiedossa. Joskus on arvioitu, että keskimääräinen ratkaisuaika olisi puolisen tuntia. Neljästä palasta (vasen kuva) syntyy T ja kuudesta palasta H. Voit tietysti tehdä oman palapelin valitsemillasi mitoilla ja jakaa kirjaimet paloiksi ihan omalla tavallasi ja tehdä pulmia muistakin kirjaimista. – Neljän T:n pulmassa on sijoitettava neljä T-kirjainta laatikkoon. Syvälahden pajutilan mallissa (oikeanpuolimmainen kuva) laatikon mitat ovat 175 × 188 mm, T-kirjaimen varsi 28 × 90 mm ja poikkiviiva 29 × 99 mm. Mahtuu kyllä vaikka ei siltä näyttäisikään. Pulmasta on monia erilaisilla mitoilla tehtyjä versioita ja laatikko voi olla pyöreäkin. Myös muita kirjaimia pakataan monenmuotoisiin laatikoihin.

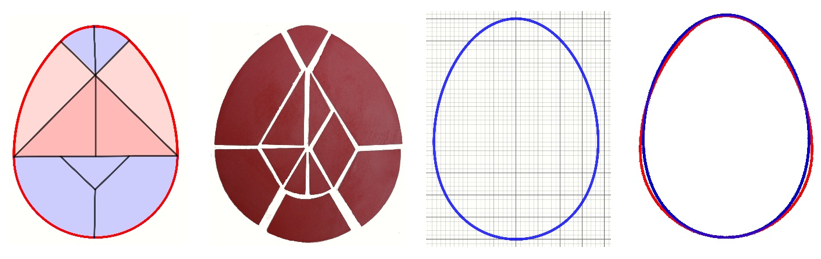
Tangramin kaltaiseen ideaan perustuu kiinalainen muna. Se koostuu isosta puoliympyränkaaresta, munan toisessa päässä olevasta pienemmästä neljännesympyränkaaresta ja niiden välillä olevista kahdesta kahdeksasosaympyränkaaresta [2]. Kuvio jaetaan tavallisesti keskiviivan suhteen symmetrisesti yhdeksään osaan, vaikka muitakin jakoja esiintyy. Paloista voidaan koota muna, mutta myös monia siluettihahmoja tangramin tapaan. Kun askartelet oman munasi paperista, pahvista tai vanerista, niin voit jakaa sen haluamallasi tavalla. Munan reunana voit käyttää myös munakäyrää [3] (siniset soikiot). Se voidaan säätää muistuttamaan hyvin läheisesti geometrista munaa (punainen soikio), mutta sillä saa aikaan monen muunkinlaisia munia.
Viisneliöt [4] (engl. pentominoes [5]) ovat monikulmioita, jotka muodostuvat viidestä vierekkäin asetetusta neliöstä. Jokaisen neliön pitää koskettaa vähintään yhtä muuta neliötä vähintään yhdellä koko sivullaan. Viisneliöitä on 12 erilaista. Keksitkö ne kaikki? Viisneliöiden yleistys ovat monineliöt (engl. polyominoes). Mahdollisten kuvioiden lukumäärä kasvaa nopeasti neliöiden määrän lisääntyessä. Niinpä esimerkiksi kahdeksanneliöitä (engl. octomino) on 369, niistä yksi seuraavassa kuvassa oikeanpuolimmaisena. Monineliöt ovat suosittu osa metkaa matematiikkaa (engl. recreational mathematics). Niinpä niitä on tutkittu paljon. Esimerkiksi google-haku ”polyomino” antaa runsaat 150 000 tulosta.

Kahdentoista erilaisen viisneliön yhteinen pinta-ala on 60. Luvun jaollisuus antaisi aiheen olettaa, että viisneliöistä voidaan koota useita erilaisia suorakulmioita. Niin onkin asianlaita. Mahdollisia ovat 3 · 20, 4 · 15, 5 · 12 ja 6 · 10. Osaatko tehdä ne? Voit pohtia, miksi muita ei ole. Esimerkiksi 6 · 10 -suorakulmion kokoamisen pitäisi olla hyvin helppoa, sillä ratkaisumahdollisuuksia on 2339. Kuinka monta erilaista sinä keksit? Monia muitakin kuvioita voidaan koota, esimerkiksi 8 · 8 -neliö, jonka keskellä on 2 · 2 -reikä. Kahdeksanneliöissä on 6 reiällistä. Muitakin kuvioita saadaan aikaan, jos ei vaadita, että kaikki viisneliöt on käytettävä. Esimerkiksi tasavartinen risti syntyy yhdeksästä viisneliöstä.
Monikuutiot (engl. polycubes [6]) mainitaan usein monineliöiden yhteydessä. Ne ovat kolmiulotteisia, sillä ne koostuvat kuutioista, jotka liittyvät muihin kuutioihin vähintään yhdellä sivutahkollaan. Rakentelukuutiot ovat erinomainen väline niiden tutkimiseen. Tarkempaan rakenteluun kannattaa tehdä neli– tai viiskuutioita esimerkiksi liimaamalla yhteen puukuutioita.

Somakuutio koostuu niistä kolmi- ja nelikuutioista, jotka eivät ole suorakulmaisia särmiöitä [7]. Ne voidaan koota kuutioksi 240 eri tavalla. Kuutio voidaan rakentaa myös pelkistä tulitikuista. Täysin ilman liimaa!

Pulmaesineiden valmistamiseen ovat tuoneet täysin uusia mahdollisuuksia 3D-tulostimet. Ne muuttavat valmistustavan käsityöstä ohjelmoinniksi. Esimerkiksi monikuutioita voidaan tulostaa yhtenä kokonaisuutena.

Lähteitä ja lisää luettavaa:
[1] Pulmasivu Pääskynen 1936. Dimensio 6/2014: 67.
[2] Geogebra-matletti Euclidean-egg-step-construction osoitteessa https://www.geogebra.org/m/wYjcsZ8e
[3] Geogebra-matletti Muna ja munakäyrä osoitteessa https://www.geogebra.org/m/hnxnbstp
[4] Pulmasivu Viisneliöitä. Dimensio 4/2013 s. 67.
[5] Wikipedia-artikkeli Pentomino osoitteessa https://en.wikipedia.org/wiki/Pentomino Älä lue tätä, jos haluat ratkaista viisneliötehtäviä itsenäisesti.
[6] Wikipedia-artikkeli Polycubes osoitteessa https://en.wikipedia.org/wiki/Polycube
[7] Wolfram Math World Soma cube osoitteessa https://mathworld.wolfram.com/SomaCube.html