Antikens Grekland – demokratins vagga
”Vandringar i antikens värld” – ett tvärvetenskapligt projekt i matematik, filosofi och modersmål
Under denna vår 2019 kommer 15 studerande från Brändö gymnasium och 10 studerande från Gymnasiet Lärkan i Helsingfors att delta i en gemensam tvärvetenskaplig kurs i matematik, filosofi och modersmål. Vi har några seminariedagar under vårens lopp och kursen utmynnar i en gemensam studieresa till Aten i början av maj. Underetcknad jobbar som lektor i matematik vid Brändö gymnasium och är en av initiativtagarna till denna kurs. Vi gjorde ett liknande projekt internt med ämnena matematik och filosofi i Brändö gymnasium förra läsåret och det utföll mycket väl. Nu utvidgar vi projektet till att omfatta ett annat svenskspråkigt gymnasium och ämnet modersmål.
De huvudsakliga målen med kursen är:
- att erbjuda ökade kunskaper och fördjupade insikter om den västerländska vetenskapens och konstens rötter med fokusering på filosofi, matematik och modersmål.
- att utveckla kompetensen i matematik, filosofi och multilitteracitet och förmågan att se tvärvetenskapliga samband mellan de tre olika disciplinernas sätt att förklara, förstå och gestalta verkligheten.
- att utveckla förmågan att kommunicera muntligt och skriftligt och att samarbeta i olika miljöer med studerande, lärare, forskare och skribenter i olika läroämnen och skolsamfund.
Det centrala innehållet i kursen omfattar
- att bekanta sig med ett urval antika filosofiska teorier, litterära verk och matematiska problem.
- att producera egna teoretiska översikter och/eller konstnärliga produkter med utgångspunkt i de vetenskapliga matematiska rön och litterära alster som producerades under denna tid.
- att presentera resultatet av denna inlärningsprocess på ort och ställe, i en geografiskt autentisk miljö.
- att presentera sina erfarenheter under resan antingen muntligt, skriftlig eller audiovisuellt (t.ex. i form av ett föredrag, medietexter, posters, dramatisering, en bildberättelse eller dokumentär).

Ett plock ur två seminariedagar i mars och april avslöjar bl.a. följande teman:
- Fibonacci och det gyllene snittet
- Grekisk metafysik
- Sokratisk dialog
- Pythagoras-Platon-Euklides-övningar
- Grekisk litteratur
- Platspresentationer
Min startkontribution ur matematisk synvinkel är bl.a. att debattera Fibonnaci och det gyllene snittet och sambandet mellan dessa. Vi talar om ”mysteriet Fi”, det gyllene snittet. Några aspeketer jag brukar ta upp här är att
- Naturen gömmer stora mysterier. ”Fi” finns i binas släktträd, aktiemarknaders variationsmönster, molnformationer för orkaner, DNA-nukleotider…
- En sköldpadda har 13 hornsköldar på sitt skal, 5 centrerade, 8 längs kanterna, 5 klor och 34 ryggradselement. Det finns 144 ryggkotor i en gabonhuggorm, en hyena har 34 tänder och en delfin 233. Många spindlar har 5 par extremiteter, 5 delar på varje extremitet och en magsäck delad i 8 segment osv.
- Platon antydde i sina skrifter att det fanns en ”gyllene nyckel” som beskrev sambandet mellan mysterierna.
- Fi definierades först av Euklides (325-265 f.Kr.)
- Tidigaste kända behandlingen av ämnet är ”Divina Proportione” av munken Luca Pacioli (1445-1517) som berusades av skönheten
- Illustrerad av Leonardo da Vinci som myntade begreppet ”sectio aurea”
- Första gången uppträder uttrycket i tryck 1835 i Pure Elementary Mathematics av Martin Ohm.
- Det finns många namn för detta ”snitt”
- I matematiken vanligt med ”Stora Fi” eller ”Lilla Fi”.
- Grekiska skulptören Phidia använde uttrycket i byggandet av Parthenon.
- Fråga: Finns det en delning där delar kan bibehålla ett meningsfullt förhållande till helheten?
- Platon (427–347 f.Kr.) bad i ”Republiken” folket ”ta en linje och dela den ojämnt…”.
- Ordet ”förhållande” blev viktigt.
- Platon ansåg att den kontinuerliga geometriska proportionen är den djupaste kosmiska bindningen. Förhållandena 1:2 och 4:8 och 1:3 samt 3:9
- Jfr ”geometriskt medelvärde” i matematiken: $b = \sqrt {a*c} $.
- Platon: ”Helheten i förhållande till den längre delen = den längre delen i förhållandet till den kortare delen.
- Pythagoreerna gillade ”harmoniska delningar”
- $\frac{1}{x} = \frac{x}{{1 – x}}$ ger 2 lösningar $x = \frac{{\sqrt 5 – 1}}{2} \approx 0,618 = g\;\;$ ${\rm{och\;\;}}x = – \frac{{\sqrt 5 + 1}}{2} \approx – 1,618 = – G{\rm{\;}}$
- Vi kan visa att $G = 1 + g$ och $g = \frac{1}{G}$
- Om längden av ”mellandelen” =1, så är den kortare delen $g$ och den längsta delen $G$.

Ett givet tema under kursen är ju också grekiska bokstäver och siffror. Talsystemet använde de 24 bokstäverna i det nuvarande grekiska alfabetet, samt tre äldre bokstäver för att beteckna tal. De första nio symbolerna fick då beteckna talen 1–9, nästa nio betecknade tiotalen 10–90 och de sista nio hundratalen 100–900. Ingen symbol för talet noll fanns. Talen bildades sedan additivt utifrån dessa symboler.

Mellan våra seminariedagar får eleverna uppgifter att göra i matematik, filosofi och modersmål. I matematiken brukar jag servera uppgifter som ungefär ser ut så här:
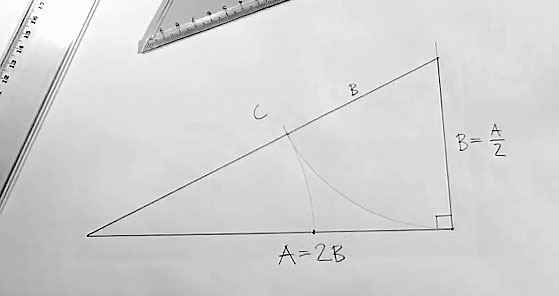
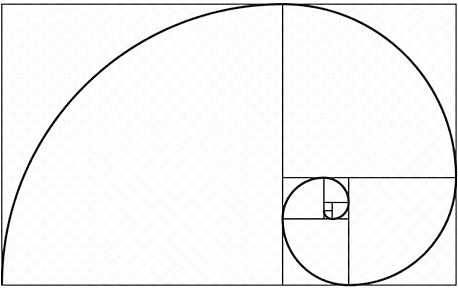
- Rita en Fibonaccispiral på rutigt papper. Börja med att rita en Fibonaccirektangel utgående från talföljden.
Låt din sista rektangel bli 13 x 34 rutor. Rita spiralen med hjälp av passare.
Hjälp online:
- Rita en ”perfekt 5-uddig stjärna”.

Kolla först:
Vilket skulle tyda på att ….. ${\Phi ^n} = {F_n} \cdot \Phi + {F_{n – 1}}$, eller hur?
- Rita en regelbunden femhörning ABCDE med sidlängden 1. Bestäm längden av diagonalen AC.
- Rita en cirkel och en bild av den ”gyllene vinkeln” i cirkeln. Hur stor är vinkeln?
Jag brukar sedan avrunda matematikdelen med ett sammanhängande avsnitt ur matematikens historieutveckling där jag tar upp bl.a. följande teman:
- KLASSISK TID (500f.Kr – 338 f.Kr)
- HELLENISTISK TID (338 f.Kr – 30 f.Kr)
- ROMERSK TID (30 f.Kr – 395 e.Kr)
- Det var under den Hellenistiska tiden matematiken blomstrade! Alexandria grundades som ”kunskapscentrum”.
- Det fanns två beteckningssystem under antiken: det attiska systemet och det joniska systemet
- Attiska systemet: Vissa bokstäver kunde kombineras för att få det önskade talet
- Joniska systemet: Använde sig av det grekiska alfabetet som siffror
Och givetvis talar vi om stora namn som Thales, Euklides, Pythagoras, Aristoteles för att nämna några. Det har varit väldigt trevligt att planera denna kurs tillsammans med mina kolleger och jag hoppas att vi i gymnasiet kan fortsätta med dessa temastudiekurser även framöver. Jag rekommenderar detta arbetssätt varmt till alla ni som vill pröva på att koppla matematiken till det verkliga livet utanför klassrummet.